Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài giải
a,
\(\widehat{DAC}=\widehat{BAD}=\widehat{DBI}\)( AD là tia phân giác \(\widehat{BAC}\) )
\(\widehat{ADC}=\widehat{BDI}\)
\(\Rightarrow\Delta ADC\sim\Delta BDI\left(g.g\right)\)
b, \(\Delta ADC\sim\Delta BDI\left(cmt\right)\Rightarrow\widehat{AIB}=\widehat{ACD}\)
\(\widehat{BAD}=\widehat{DAC}\)
\(\Rightarrow\Delta ABI\sim\Delta ADC\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AI}=\dfrac{AD}{AC}\Rightarrow AB.AC=AD.AI\)
a: Xét ΔDAB và ΔDCI có
góc DAB=góc DCI
góc ADB=góc CDI
=>ΔDAB đồng dạng với ΔDCI
=>DA/DC=DB/DI
=>DA/DB=DC/DI
Xét ΔDAC và ΔDBI có
DA/DB=DC/DI
góc ADC=góc BDI
=>ΔDAC đồng dạng với ΔDBI
b: Xét ΔABD và ΔAIC có
góc ABD=góc AIC
góc bAD=góc IAC
=>ΔABD đồng dạng với ΔAIC
=>AB/AI=AD/AC
=>AB*AC=AD*AI
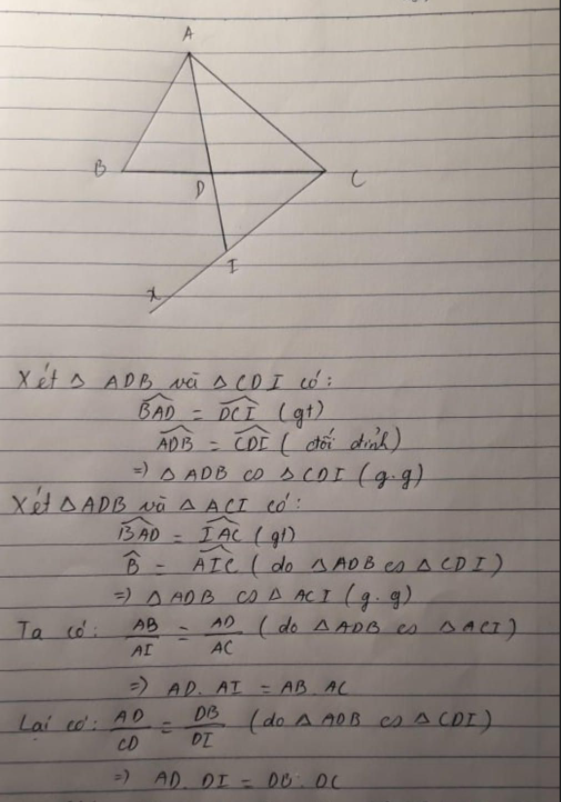
a, Xét tam giác ADB và tam giác CDI có:
góc ADB = góc CDI (đối đỉnh)
góc BAD = góc DCI (gt)
Do đó: Tam giác ADB đồng dạng với tam giác CDI (g.g) (1)
Suy ra: góc ABD = góc DIC
b, Tam giác ADB đồng dạng với tam giác ACI (g.g) (2)
Suy ra: AD/AC = AB/AI
c, Từ (1),ta thấy: AD/CD = DB/DI nên AD.DI = BD.BC
Từ (2),ta có: AD/AC = AB/AI nên AD.AI = AB.AC
Do đó: AD(AI-DI) = AB.AC - BD.BC
AD^2 = AB.AC -BD.BC
Bài bạn đưa ra hơi khó đấy.Chúc bạn học tốt.
Cảm ơn bn nhiều lắm :3