Gấp ạ!!! Làm câu c thôi ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
\(a,\) Gọi \(\left(d\right):y=ax+b\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\0a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\Leftrightarrow\left(d\right):y=2x+1\)
\(b,\) PT hoành độ giao điểm:
\(-x^2=2x+1\Leftrightarrow\left(x+1\right)^2=0\Leftrightarrow x=-1\Leftrightarrow y=-1\Leftrightarrow A\left(-1;-1\right)\)
Vậy \(A\left(-1;-1\right)\) là tọa độ giao điểm (P) và (d)
Bài 4:
PT có 2 nghiệm \(\Leftrightarrow\Delta'=16-3m\ge0\Leftrightarrow m\le\dfrac{16}{3}\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{8}{3}\\x_1x_2=\dfrac{m}{3}\end{matrix}\right.\)
Mà \(x_1^2+x_2^2=\dfrac{82}{9}\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=\dfrac{82}{9}\)
\(\Leftrightarrow\dfrac{64}{9}-\dfrac{2m}{3}=\dfrac{82}{9}\\ \Leftrightarrow\dfrac{2m}{3}=-2\Leftrightarrow m=-3\left(tm\right)\)

\(1,=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=2\left(x^2+2x+1-y^2\right)=2\left[\left(x+1\right)^2-y^2\right]\\ =2\left(x+y+1\right)\left(x-y+1\right)\\ 5,=16-\left(x-y\right)^2=\left(4-x+y\right)\left(4+x-y\right)\)

2) \(=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\)
3) \(=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\)
4) \(=2\left[\left(x^2+2x+1\right)-y^2\right]=2\left[\left(x+1\right)^2-y^2\right]\)
\(=2\left(x+1-y\right)\left(x+1+y\right)\)
5) \(=16-\left(x^2-2xy+y^2\right)=16-\left(x-y\right)^2\)
\(=\left(4-x+y\right)\left(4+x-y\right)\)



a: góc AMB=1/2*180=90 độ
góc AMN+góc AKN=180 độ
=>AMNK là tứ giác nội tiếp
b: ΔCAB vuông tại A có AM vuông góc CB
nên CA^2=MC*CB

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB


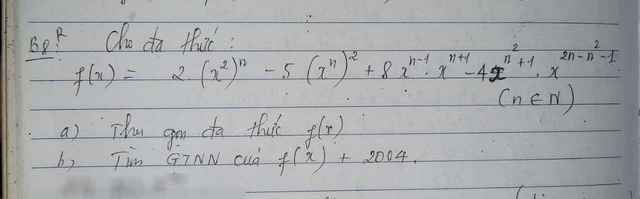


 vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á
vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á

c: Ta có: AM//BC
AE⊥BC
Do đó:AM⊥AE
Suy ra: \(\widehat{AME}+\widehat{AEM}=90^0\)
hay \(\widehat{AME}+\widehat{BAD}=90^0\)