cho tứ giác lồi abcd,gọi m,n là trung điểm ab,cd.cmr:2mn=ad+bc giúp em với ạaa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QA
0
29 tháng 7 2021
Ta có : Tứ giác MPNQ là hình bình hành
MN và PQ cắt nhau tại trung điểm I của mỗi đường
Ta có : Tứ giác EPFQ là hình bình hành
EF đi qua I
Vậy EF , MN và PQ đồng quy
CM
5 tháng 12 2017
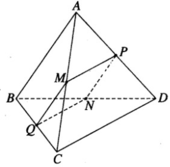
Ta có MPNQ là hình bình hành vì
Do đó
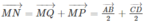
hay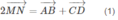 
Mặt khác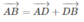 
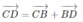
Nên
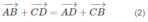
Vì
Từ (1) và (2) ta có:
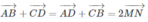
là đẳng thức cần chứng minh
P
0
27 tháng 10 2021
Xét ΔABC có
E là trung điểm của AB
N là trung điểm của AC
Do đó: EN là đường trung bình của ΔABC
Suy ra: EN//BC và \(EN=\dfrac{BC}{2}\left(1\right)\)
Xét ΔBDC có
M là trung điểm của BD
F là trung điểm của CD
Do đó: MF là đường trung bình của ΔBDC
Suy ra: MF//BC và \(MF=\dfrac{BC}{2}\left(2\right)\)
Xét ΔABD có
E là trung điểm của AB
M là trung điểm của BD
Do đó: EM là đường trung bình của ΔABD
Suy ra: \(EM=\dfrac{AD}{2}=\dfrac{BC}{2}\left(3\right)\)
Từ (1) và (2) suy ra EN//MF và EN=MF
Từ (1) và (3) suy ra EN=EM
Xét tứ giác ENFM có
EN//MF
EN=MF
Do đó: ENFM là hình bình hành
mà EN=EM
nên ENFM là hình thoi
29 tháng 11 2017
Bạn tra gu gồ được mà,hỏi làm gì cho mệt chớ,tìm được cách làm trên gu gồ là áp dụng vào bài thôi
LV
29 tháng 11 2017
noi A vs C ,BvsC
ap dung tinh chat duong trug binh cua tam giac
AM=EN
MN=FE
MNEF la hinh thoi
