Giúp e câu 4 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
0
23 tháng 7 2021
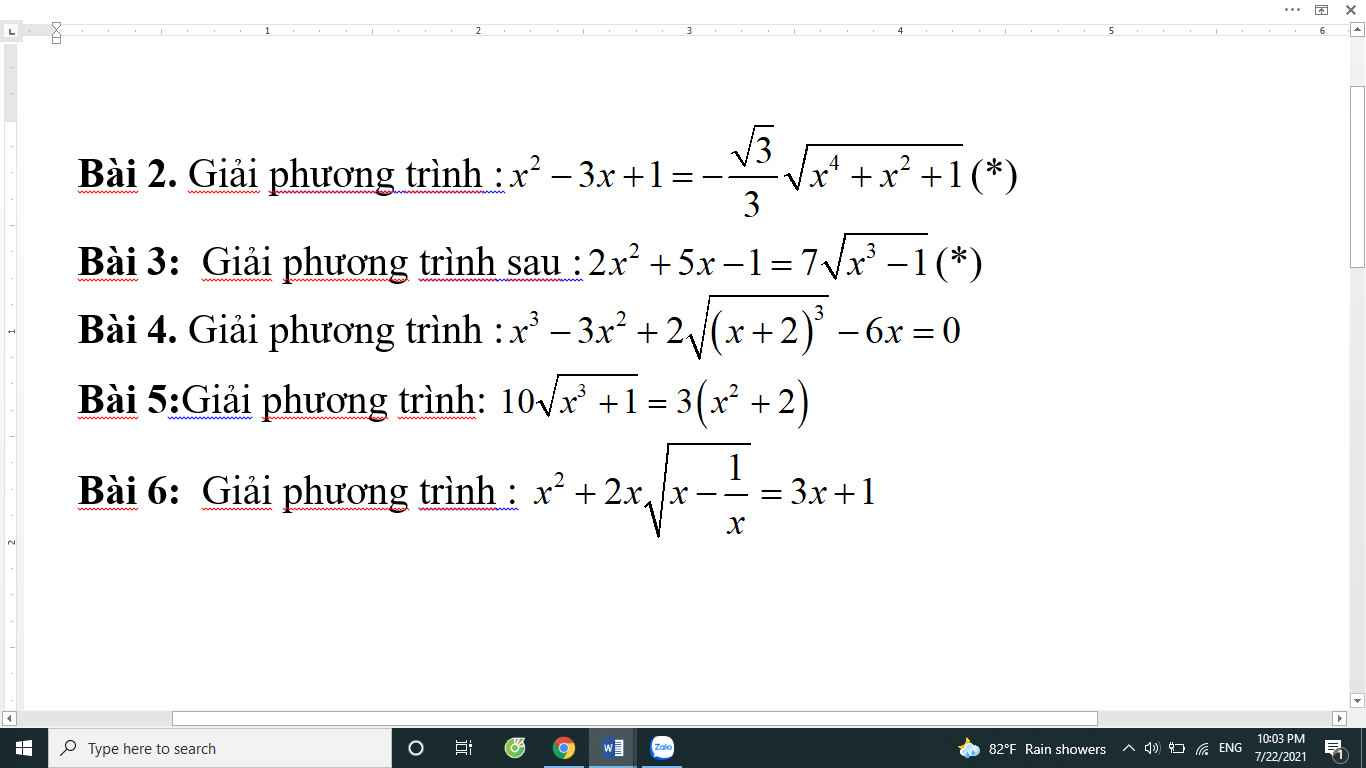
Đặt \(\sqrt{x^2-x+1}=a>0;\sqrt{x^2+x+1}=b>0\).
\(PT\Leftrightarrow2a^2-b^2=-\dfrac{\sqrt{3}}{3}ab\)
\(\Leftrightarrow\left(a+\dfrac{\sqrt{3}}{2}b\right)\left(2a-\dfrac{2\sqrt{3}}{3}b\right)=0\)
\(\Leftrightarrow2a-\dfrac{2\sqrt{3}}{3}b=0\) (Do a, b > 0)
\(\Leftrightarrow2\sqrt{x^2-x+1}=\dfrac{2\sqrt{3}}{3}\sqrt{x^2+x+1}\)
\(\Leftrightarrow x^2-x+1=\dfrac{1}{3}\left(x^2+x+1\right)\Leftrightarrow2x^2-4x+2=0\Leftrightarrow x=1\).
Vậy x = 1
11 tháng 3 2022
Câu 3.
Ảnh thật, ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\)
\(\Rightarrow d'=30cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{1}{h'}=\dfrac{15}{30}\Rightarrow h'=2cm\)
Câu 4.
Ảnh ảo, cùng chiều và nhỏ hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{8}\)
\(\Rightarrow d'=4,8cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{2}{h'}=\dfrac{8}{4,8}\Rightarrow h'=1,2cm\)
Khoảng cách từ vật đến ảnh:
\(AA'=8-4,8=3,2cm\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
7 tháng 4 2023
Đổi 1,672m= 167,2cm
167,2cm gấp 88cm số lần là:
167,2:88= 1,9(lần)
Bánh xe sau lăn được 50 vòng thì bánh xe trước lăn được:
50 x 1,9= 95(vòng)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 4 2023
Bán kính đáy: 12:2=6(cm)
Thể tích nước dâng lên bằng thể tích tượng đá nên thể tích tượng đá là:
\(V=\pi.6^2.2,56\approx290\left(cm^3\right)=290\left(ml\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
Tiền lời khi bán 1 đôi giày: \(x-30\) (đô la)
Số tiền lời mà cửa hàng thu được:
\(\left(x-30\right)\left(80-x\right)=-x^2+110x-2400=-\left(x-55\right)^2+625\le625\)
Dấu "=" xảy ra khi \(x-55=0\Leftrightarrow x=55\)
Vậy cửa hàng bán với giá 55 đô la 1 đôi giày sẽ thu được lời lớn nhất
NT
3
Qua A kẻ đường thẳng vuông góc AI cắt CD kéo dài tại E
Ta có \(\widehat{EAD}=\widehat{MAB}\) (cùng phụ \(\widehat{DAM}\))
\(\Rightarrow\Delta_vADE\sim\Delta_vABM\Rightarrow\dfrac{AE}{AM}=\dfrac{AD}{AB}=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{1}{AE}=\dfrac{4}{3AM}\)
Áp dụng hệ thức lượng trong tam giác vuông AEI:
\(\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AI^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{3}{4}AB\right)^2}=\left(\dfrac{4}{3AM}\right)^2+\dfrac{1}{AI^2}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{1}{AM^2}+\dfrac{9}{16AI^2}\)