Giải phương trình: \(2\text{x}^2+5\text{x}-1=7\sqrt{x^3-1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 3 2022
\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
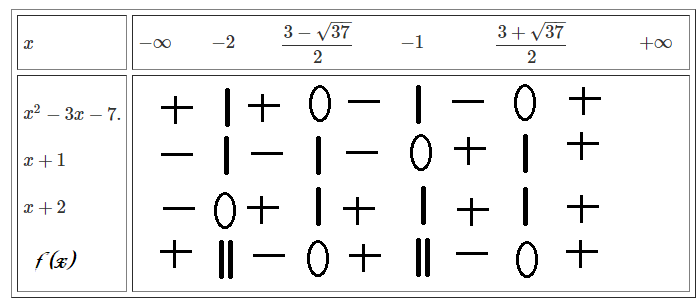
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
9 tháng 2 2023
Đặt \(t=\sqrt{10-x}+\sqrt{x-7}\) để làm gì vậy bạn? Đặt như vậy thì phương trình sẽ càng khó giải hơn á
Đk: \(-7\le x\le10\)
\(\sqrt{10-x}-\sqrt{x+7}+\sqrt{-x^2+3x+70}=1\)
\(\Leftrightarrow\sqrt{10-x}-\sqrt{x+7}+\sqrt{\left(10-x\right)\left(x+7\right)}=1\)
\(\Leftrightarrow\sqrt{10-x}\left(\sqrt{x+7}+1\right)-\left(\sqrt{x+7} +1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x+7}+1\right)\left(\sqrt{10-x}-1\right)=0\)
Dễ thấy \(\sqrt{x+7}+1>0\). Do đó:
\(\sqrt{10-x}-1=0\Leftrightarrow x=9\left(nhận\right)\)
Thử lại ta có x=9 là nghiệm duy nhất của pt đã cho.
2
9 tháng 2 2023
`\sqrt{10-x}-\sqrt{x+7}+\sqrt{-x^2+3x+70}=1` `ĐK: -7 <= x <= 10`
Đặt `\sqrt{10-x}-\sqrt{x+7}=t`
`<=>10-x+x+7-2\sqrt{(x+7)(10-x)}=t^2`
`<=>\sqrt{-x^2+3x+70}=17/2-[t^2]/2`
Khi đó ptr `(1)` có dạng: `t+17/2-[t^2]/2=1`
`<=>2t+17-t^2=2`
`<=>t^2-2t-15=0`
`<=>[(t=5),(t=-3):}`
`@t=5=>\sqrt{-x^2+3x+70}=17/2-5^2/2`
`<=>\sqrt{-x^2+3x+70}=-4` (Vô lí)
`@t=-3=>\sqrt{-x^2+3x+70}=17/2-[(-3)^2]/2`
`<=>-x^2+3x+70=16`
`<=>[(x=9),(x=-6):}` (t/m)
Vậy `S={-6;9}`
MS
0
A
0
29 tháng 8 2015
Điều kiện xác định phương trình \(x\ge\frac{1}{4}\).
Nhân cả hai vế với \(\sqrt{2}\) phương trình tương đương với
\(\sqrt{4x-2\sqrt{4x-1}}-\sqrt{4x+2\sqrt{4x-1}=4}\leftrightarrow\left|\sqrt{4x-1}-1\right|-\left|\sqrt{4x-1}+1\right|=4\)
\(\leftrightarrow\left|\sqrt{4x-1}-1\right|-\sqrt{4x-1}=5\).
Trường hợp 1. NẾU \(x\ge\frac{1}{2}\to\sqrt{4x-1}-1-\sqrt{4x-1}=5\to\) loại
Trường hợp 2. NẾU \(\frac{1}{4}\le x
