Cho đường chéo của hình chữ nhật ABCD cắt nhau tại O
Chứng minh rằng: Tứ giác EFGH có các đỉnh theo thứ tự của trung điểm OA;OB;OC;OD là hình bình
giải nhanh và vẽ hình giúp mình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 8 2016
THam khảo nha :
Xét bài toán: Cho tam giác ABC.ABC. Dựng hình vuông ABEFABEF và ACGHACGH phía ngoài tam giác. P,P, QQ theo thứ tự là tâm của hình vuông ABEFABEF và ACGH.ACGH. Lấy MMtrung điểm BC.BC. Chứng minh tam giác PQMPQM vuông cân tại M.M.
Lời giải:
Dễ dàng chứng minh được MPMP và MQMQ theo thứ tự là đường trung bình của tam giác BCFBCF và BCH.BCH.
Suy ra MP∥CF ; MP=12CFMP∥CF ; MP=12CF và MQ∥BH ; MQ=12BH. (1)MQ∥BH ; MQ=12BH. (1)
Ta có:
ˆBAH=ˆBAF+ˆFAH=90∘+ˆFAHBAH^=BAF^+FAH^=90∘+FAH^
ˆCAF=ˆCAH+ˆFAH=90∘+ˆFAHCAF^=CAH^+FAH^=90∘+FAH^
Do đó ˆBAH=ˆCAF.BAH^=CAF^.
Từ đó chứng minh được △AFC=△ABH (c.g.c)△AFC=△ABH (c.g.c)
⇒ˆFCA=ˆBHA⇒FCA^=BHA^
Gọi II và OO theo thứ tự là giao điểm của CFCF với BHBH và AH.AH.
Khi đó ˆOCA=ˆIHOOCA^=IHO^
Mà ˆOCA+ˆAOC=90∘OCA^+AOC^=90∘ và ˆAOC=ˆIOHAOC^=IOH^ ((đối đỉnh))
Nên ˆIHO+ˆIOH=90∘,IHO^+IOH^=90∘, suy ra ˆHIO=90∘HIO^=90∘
Do đó IH⊥IOIH⊥IO hay BH⊥CF. (2)BH⊥CF. (2)
Vì △AFC=△ABH (c.g.c)△AFC=△ABH (c.g.c) nên CF=BH. (3)CF=BH. (3)
Từ (1),(1), (2)(2) và (3)(3) suy ra MP=MQMP=MQ và MP⊥MQ.MP⊥MQ. Vậy tam giác MPQMPQ vuông cân tại M.M.
★★★★★★★★★★★★★★★★
Quay lại bài toán. Gọi MM là trung điểm ACAC
Áp dụng kết quả trên, ta chứng minh được tam giác EMFEMF và HMGHMG vuông cân tại M.M.
Từ đó chứng minh được △MEG=△MFH (c.g.c)△MEG=△MFH (c.g.c)
Rồi suy ra EG=HFEG=HF và EG⊥HF.EG⊥HF.
b)b) Gọi PP và QQ lần lượt là trung điểm HFHF và EGEG
Từ △MEG=△MFH (c.g.c)△MEG=△MFH (c.g.c) dễ dàng chứng minh được △MPF=△MQE (c.g.c)△MPF=△MQE (c.g.c)
Suy ra MP=MQMP=MQ và ˆPMF=ˆQME ⇒ ˆPMQ=ˆEMF=90∘PMF^=QME^ ⇒ PMQ^=EMF^=90∘
Do đó tam giác MPQMPQ vuông cân tại MM
Gọi NN trung điểm BD.BD. Chứng minh tương tự như trên, ta được tam giác NPQNPQ vuông cân tại N.N.
Suy ra tứ giác MPNQMPNQ là hình vuông.
7 tháng 12 2015
a) nối A với C , B với D được:
EF // AC ( đường trung bình của tam giác BAC)
HG // AC ( " " " " " " ) suy ra EF // AC do cùng // AC
HE // DB ( đường trung bình tam giác ADB )
FG // DB ( " " " " " " ) suy ra HE // FG do cùng // với DB
Xét tứ giác EFGH có 2 cặp cạnh đối song song nên EFGH là hình bình hành
b) EFGH là hình ....
Thoi , suy ra EH = GH nên AC=BD ( do là đường trung bình của hai tam giác ADB,ADC)
vì AC = BD nên ABCD là hình thang cân
Chữ nhật, suy ra HE vuông góc với HG nên AC vuông góc với BD
Hình vuông , kết hợp 2 yếu tố của 2 hình trên được AC=BD và AC vuông góc với BD.
Tích nha☺
CM
9 tháng 9 2019
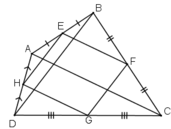
Ta có: EB = EA, FB = FC (gt)
⇒ EF là đường trung bình của ΔABC
⇒ EF // AC và EF = AC/2.
HA = HD, HC = GD
⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG = AC/2.
Do đó EF // HG, EF = HG
⇒ EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF
⇔ AC ⊥ BD (vì EH // BD, EF// AC)
b) Hình bình hành EFGH là hình thoi
⇔ EF = EH
⇔ AC = BD (Vì EF = AC/2, EH = BD/2)
c) EFGH là hình vuông
⇔ EFGH là hình thoi và EFGH là hình chữ nhật
⇔ AC = BD và AC ⊥ DB.
CM
7 tháng 10 2018
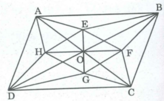
Ta có: ∠ (AOB) = ∠ (COD) (đối đỉnh)
∠ (EOB ) = 1/2 ∠ (AOB) (gt)
∠ (COG) = 1/2 ∠ (COD) (gt)
Suy ra: ∠ (EOB ) = ∠ (COG)
∠ (EOB) + ∠ (BOC) + ∠ (COG) = 2 ∠ (EOB) + ∠ (BOC)
Mà ∠ (AOB ) + ∠ (BOC) = 180 0 ( kề bù).Hay 2 ∠ (EOB) + ∠ (BOC ) = 180 0
Suy ra: E,O,G thẳng hàng
Ta lại có: ∠ (BOC) = ∠ (AOD ) ( đối đỉnh)
∠ (HOD) = 1/2 ∠ (AOD) (gt)
∠ (FOC) = 1/2 ∠ (BOC) (gt)
Suy ra: ∠ (HOD) = ∠ (FOC)
∠ (HOD) + ∠ (COD ) + ∠ (FOC) = 2 ∠ (HOD) + ∠ (COD)
Mà ∠ (AOD) + ∠ (COD) = 180 0 ( kề bù). Hay 2 ∠ (HOD) + ∠ (COD) = 180 0
Suy ra: H, O, F thẳng hàng
∠ (ADO) = ∠ (CBO) ( so le trong)
∠ (HDO) = ∠ (FBO) ( chứng minh trên)
OD = OB ( t/chất hình bình hành)
∠ (HOD) = ∠ (FOB ) ( đối đỉnh)
Do đó: ∆ BFO = ∆ DHO (g.c.g)
⇒ OF = OH
∠ (OAB) = ∠ (OCD) ( so le trong)
∠ (OAE) = 1/2 ∠ (OAB ) (gt)
∠ (OCG) = 1/2 ∠ (OCD) (gt)
Suy ra: ∠ (OAE) = ∠ (OCG)
Xét ∆ OAE và ∆ OCG,ta có :
∠ (OAE) = ∠ (OCG) ( chứng mình trên)
OA = OC ( t/chất hình bình hành)
∠ (EOA) = ∠ (GOC) ( đối đỉnh)
Do đó: ∆ OAE= ∆ OCG (g.c.g) ⇒ OE = OG
Suy ra tứ giác EFGH là hình bình hành ( vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
OE ⊥ OF (tính chất tia phân giác của hai góc kề bù) hay EG ⊥ FH
Vậy tứ giác EFGH là hình thoi
CM
4 tháng 4 2017
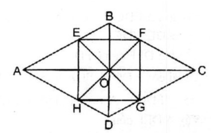
Ta có: ∠ (AOB) và ∠ (COD) đối đỉnh nên E, O, G thẳng hàng
∠ (BOC) và ∠ (AOD) đối đỉnh nên F, O, H thẳng hàng
Xét ∆ BEO và ∆ BFO:
∠ (EBO) = ∠ (FBO) (tính chất hình thoi)
OB cạnh chung
∠ (EOB) = ∠ (FOB) = 45 0 (gt)
Do đó: ∆ BEO = ∆ BFO (g.c.g)
⇒ OE = OF (1)
Xét ∆ BEO và ∆ DGO:
∠ (EBO) = ∠ (GDO) (so le trong)
OB = OD(tính chất hình thoi)
∠ (EOB) = ∠ (GOD) (đối đỉnh)
Do đó: ∆ BEO = ∆ DGO (g.c.g)
⇒ OE = OG (2)
Xét ∆ AEO và ∆ AHO:
∠ (EAO) = ∠ (HAO) (tính chất hình thoi)
OA cạnh chung
∠ (EOA) = ∠ (HOA) = 45 0 (gt)
Do đó: ∆ AEO = ∆ AHO (g.c.g)
⇒ OE = OH (3)
Từ (1), (2) và (3) suy ra: OE = OF = OG = OH hay EG = FH
nên tứ giác EFGH là hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
OE ⊥ OF (tính chất tia phân giác của hai góc kề bù)
hay EG ⊥ FH
Vậy hình chữ nhật EFGH là hình vuông.
21 tháng 4 2017
Ta có : HE, GF lần lượt là đường trung bình của tam giác ADB và tam giác CDB
=> HE // BD, GF // BD và BD = 2HE = 2GF
Tương tự : HG, EF lần lượt là đường trung bình của tam giác DAC và tam giác BAC
=> HG // AC, EF // AC và AC = 2HG = 2EF
Nên EFGH là hình bình hành.
a) Đề hình bình hành EFGH là hình chữ nhật thì EH ⊥ EF => BD ⊥ AC
Điều kiện phải tìm : Hai đường chéo AC, BD vuông góc với nhau.
b) Để hình bình hành EFGH là hình thoi thì EH = EF => BD = AC
Điều kiện phải tìm : Hai đường chéo AC và BD bằng nhau.
c) Để hình bình hành EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật, vừa là hình thoi => BD ⊥ AC và BD = AC.
Điều kiện phải tìm : Hai đường chéo AC, BD vuông góc với nhau và bằng nhau.
