Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tứ giác có thể là hình vuông, chữ nhật phải không bạn?
P/s: Hỏi thôi chớ không trả lời đâu :D

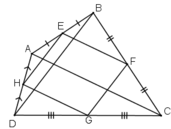
Ta có: EB = EA, FB = FC (gt)
⇒ EF là đường trung bình của ΔABC
⇒ EF // AC và EF = AC/2.
HA = HD, HC = GD
⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG = AC/2.
Do đó EF // HG, EF = HG
⇒ EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF
⇔ AC ⊥ BD (vì EH // BD, EF// AC)
b) Hình bình hành EFGH là hình thoi
⇔ EF = EH
⇔ AC = BD (Vì EF = AC/2, EH = BD/2)
c) EFGH là hình vuông
⇔ EFGH là hình thoi và EFGH là hình chữ nhật
⇔ AC = BD và AC ⊥ DB.

a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//BD và \(EH=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của DC
Do đó: FG là đường trung bình của ΔBCD
Suy ra: FG//BD và \(FG=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành


Ta có : HE, GF lần lượt là đường trung bình của tam giác ADB và tam giác CDB
=> HE // BD, GF // BD và BD = 2HE = 2GF
Tương tự : HG, EF lần lượt là đường trung bình của tam giác DAC và tam giác BAC
=> HG // AC, EF // AC và AC = 2HG = 2EF
Nên EFGH là hình bình hành.
a) Đề hình bình hành EFGH là hình chữ nhật thì EH ⊥ EF => BD ⊥ AC
Điều kiện phải tìm : Hai đường chéo AC, BD vuông góc với nhau.
b) Để hình bình hành EFGH là hình thoi thì EH = EF => BD = AC
Điều kiện phải tìm : Hai đường chéo AC và BD bằng nhau.
c) Để hình bình hành EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật, vừa là hình thoi => BD ⊥ AC và BD = AC.
Điều kiện phải tìm : Hai đường chéo AC, BD vuông góc với nhau và bằng nhau.

a) nối A với C , B với D được:
EF // AC ( đường trung bình của tam giác BAC)
HG // AC ( " " " " " " ) suy ra EF // AC do cùng // AC
HE // DB ( đường trung bình tam giác ADB )
FG // DB ( " " " " " " ) suy ra HE // FG do cùng // với DB
Xét tứ giác EFGH có 2 cặp cạnh đối song song nên EFGH là hình bình hành
b) EFGH là hình ....
Thoi , suy ra EH = GH nên AC=BD ( do là đường trung bình của hai tam giác ADB,ADC)
vì AC = BD nên ABCD là hình thang cân
Chữ nhật, suy ra HE vuông góc với HG nên AC vuông góc với BD
Hình vuông , kết hợp 2 yếu tố của 2 hình trên được AC=BD và AC vuông góc với BD.
Tích nha☺