Cho tam giác 𝐴𝐵𝐶: 𝐴𝐵 = 35, 𝐴𝐶 = 20, góc 𝐴 = 60 độ . a) Tính chiều cao kẻ từ đỉnh 𝐴 của tam giác 𝐴𝐵𝐶. b) Tính 𝐵𝐶. c) Kẻ đường kính 𝐵𝐷 của đường tròn ngoại tiếp tam giác 𝐴𝐵𝐶. Tính góc 𝐵𝐷𝐶 , BD và suy ra bán kính đường tròn ngoại tiếp tam giác 𝐴𝐵𝐶.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 4 2023
a: Xet ΔABC và ΔEBA có
góc BAC=góc BEA
góc B chung
=>ΔABC đồng dạng với ΔEBA
b: ΔABC vuông tại A có AE vuông góc BC
nên AB^2=BE*BC
c: BF là phân giác
=>AF/AB=CF/BC
=>AF/3=FC/5=4/8=1/2
=>AF=1,5cm
KV
24 tháng 4 2023
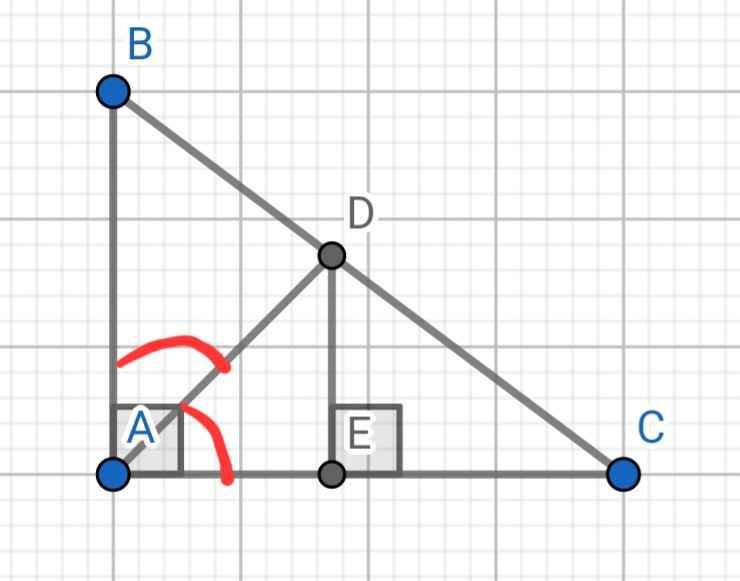
a) Do AD là đường phân giác của ∠BAC
⇒ BD/CD = AB/AC = 9/12 = 3/4
b) Xét hai tam giác vuông: ∆ABC và ∆EDC có:
∠C chung
⇒ ∆ABC ∽ ∆EDC (g-g)
24 tháng 4 2023
a: BD/CD=AB/AC=3/4
b: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEDC
26 tháng 1 2022
a: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
Xét ΔADE có AD=AE
nên ΔADE cân tại A
b: Xét ΔABC có
D là trung điểm của AB
DF//AC
Do đó: F là trung điểm của BC
Xét ΔABC có
D là trung điểm của AB
F là trung điểm của BC
Do đó: DF là đường trung bình
=>DF=AE
mà AE=AD
nên DF=AD
=>ΔADF cân tại D
c: Xét tứ giác ADFE có
DF//AE
DF=AE
Do đó: ADFE là hình bình hành
mà AD=AE
nên ADFE là hình thoi
=>AF⊥DE
AT
14 tháng 7 2021
a) tam giác AEB vuông tại E có EH là đường cao \(\Rightarrow BH.BA=BE^2\)
tam giác CEB vuông tại E có EK là đường cao \(\Rightarrow BK.BC=BE^2\)
\(\Rightarrow BH.BA=BK.BC\)
b) \(BH.BA=BK.BC\Rightarrow\dfrac{BH}{BC}=\dfrac{BK}{BA}\)
Xét \(\Delta BHK\) và \(\Delta BCA:\) Ta có: \(\left\{{}\begin{matrix}\angle ABCchung\\\dfrac{BH}{BC}=\dfrac{BK}{BA}\end{matrix}\right.\)
\(\Rightarrow\Delta BHK\sim\Delta BCA\left(c-g-c\right)\)
b) \(\Delta BHK\sim\Delta BCA\Rightarrow\angle BHK=\angle BCA\)
Kẻ \(ED\bot CF\)
Vì \(\angle EHF=\angle EDF=\angle HFD=90\Rightarrow EHFD\) là hình chữ nhật
\(\Rightarrow HD\) và EF cắt nhau tại trung điểm I của mỗi đường
Vì \(\Delta EHF\) vuông tại H có I là trung điểm EF
\(\Rightarrow\angle FHI=\angle HFI=\angle AFE\left(1\right)\)
Xét \(\Delta AFC\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle AFC=\angle AEB=90\end{matrix}\right.\)
\(\Rightarrow\Delta AFC\sim\Delta AEB\left(g-g\right)\Rightarrow\dfrac{AF}{AE}=\dfrac{AC}{AB}\Rightarrow\dfrac{AF}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\dfrac{AF}{AC}=\dfrac{AE}{AB}\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c-g-c\right)\Rightarrow\angle AFE=\angle ACB\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\angle FHI=\angle ACB=\angle BHK\Rightarrow\angle BHD=BHK\)
\(\Rightarrow H,D,K\) thẳng hàng \(\Rightarrow H,I,K\) thẳng hàng
14 tháng 7 2021
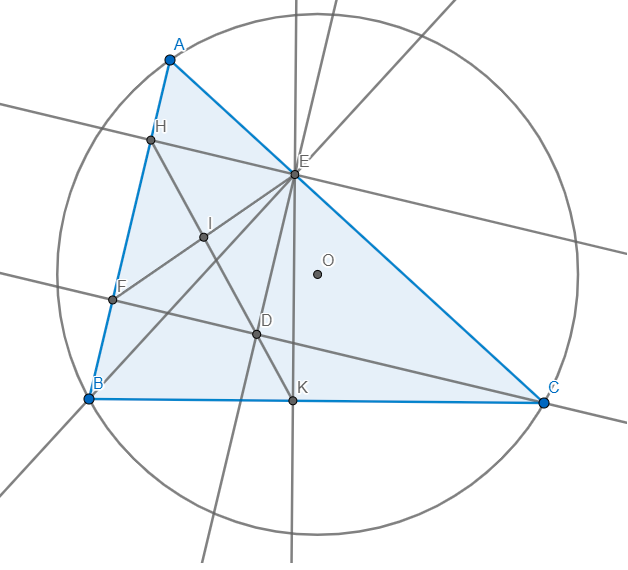
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔBEA vuông tại E có EH là đường cao ứng với cạnh huyền AB, ta được:
\(BH\cdot BA=BE^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBEC vuông tại E có EK là đường cao ứng với cạnh huyền AC, ta được:
\(BK\cdot BC=BE^2\)(2)
Từ (1) và (2) suy ra \(BH\cdot BA=BK\cdot BC\)
b) Xét ΔBHK và ΔBCA có
\(\dfrac{BH}{BC}=\dfrac{BK}{BA}\)(cmt)
\(\widehat{HBK}\) chung
Do đó: ΔBHK\(\sim\)ΔBCA(c-g-c)
13 tháng 2 2022
a, Nửa chu vi là \(\frac{6+6+6}{2}=9cm\)
Diện tích tam giác là \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{9\left(9-6\right)\left(9-6\right)\left(9-6\right)}\)
\(=\sqrt{9.3.3.3}=9\sqrt{3}\)cm2
b, Xét tam giác ABC vuông tại A
tan^B = \(\frac{AC}{AB}\Rightarrow\frac{\sqrt{3}}{3}=\frac{2}{AB}\Rightarrow AB=\frac{6\sqrt{3}}{3}=2\sqrt{3}\)cm
Diện tích tam giác là \(\frac{1}{2}AB.AC=6\sqrt{3}\)cm2
c, Dựng AH là đường cao đồng thời là đường trung tuyến do tam giác ABC cân tại A
=> HC = BC/2 = 3 cm
Theo định lí Pytago tam giác AHC vuông tại H
\(AH=\sqrt{AC^2-HC^2}=4cm\)
Diện tích tam giác ABC là : \(\frac{1}{2}AH.BC=\frac{4.6}{2}=12cm^2\)
S
9 tháng 9 2021
b) xét tg DHC và tg BAC có A=H =90 độ
C chung
=> tg DHC ~ tg BAC( g.g)
=> \(\dfrac{CH}{AC}=\dfrac{CD}{BC}=>CH.CB=CD.CA\)
c) ta có AC=AD+DC => DC=AC-AD=20-9,4=10,6 cm
tg DHC~ tg BAC => \(\dfrac{SDHC}{SBAC}=\left(\dfrac{DC}{BC}\right)^2=\left(\dfrac{10,6}{25}\right)^2\)
=> SDHC= SBAC.\(\left(\dfrac{10,6}{25}\right)^2\)
Chỗ này bạn thay số và tính nhé
S
9 tháng 9 2021
a) Xét ABC cos A=90 độ=> BC2=AC2+AB2( dl Py ta go)
=> BC2= 202+152=625 => BC=25 cm
Xét tg ABC có BD pg B
\(\dfrac{AB}{BC}=\dfrac{AD}{DC}=>\dfrac{AB}{BC+AB}=\dfrac{AD}{AD+DC}< =>\dfrac{15}{15+20}=\dfrac{AD}{BC}< =>\dfrac{15}{35}=\dfrac{AD}{25}=>AD=\dfrac{15.25}{35}~~9,4cm\)
