cho hai đường thẳng y=2x+4 (d) và y=-x+3 (d')
a) vẽ mặt phẳng tọa độ và gọi A là giao điểm (d) và (d'). tìm tọa độ của điểm A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
Cho hai đường thẳng d: y = x + 3 và d': y = -2x . Khi đó:
A. d // d'
B. d ≡ d'
C. d cắt d'
D. d ⊥ d'
1
CM
31 tháng 10 2018
Đáp án C
Ta thấy d: y = x + 3 có a = 1 và d': y = -2x có a' = -2 ⇒ a ≠ a' (1 ≠ -2) nên d cắt d'
CM
26 tháng 1 2017
Ta thấy d : y = x + 3 c ó a = 1 v à d ’ : y = − 2 x c ó a ’ = − 2
a ≠ a ’ ( 1 ≠ − 2 ) nên d cắt d’
Đáp án cần chọn là: C
PT
Cho hai đường thẳng d: y = x + 3 và d': y = -2x . Khi đó:
A. d // d'
B. d ≡ d'
C. d cắt d'
D. d ⊥ d'
1
CM
6 tháng 2 2017
Đáp án C
Ta thấy d: y = x + 3 có a = 1 và d': y = -2x có a' = -2 ⇒ a ≠ a' (1 ≠ -2) nên d cắt d'
NC
0
22 tháng 11 2015
a) x =-2 d' => y =2(-2) -1 =-5 => M(-2;-5)
d cắt d' tại M =>k khác 2 và M thuộc (d) => k.(-2) -4 =-5 => -2k = -1 => k =1/2 (TM)
b) + Phương trình hoành độ giao điểm của d1 và d2 là:
3x =x+2 => x =1
với x =1 (d1) => y =3 => d1 cắt d2 tại N(1;3)
Để 3 đường thẳng đồng quy thì d3 qua N => (m-3).1 +2m +1 =3 => m -3 +2m +1 =3 => 3m =5 => m =5/3
CM
11 tháng 5 2019
Đáp án B
+Giao điểm của d và là nghiệm của hệ
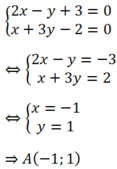
+Lấy M(0; 3) thuộc d. Tìm M’ đối xứng M qua
Viết phương trình đường thẳng đi qua M(0;3) và vuông góc với :
3( x-0) -1( y-3) =0 hay 3x –y+3= 0
+Gọi H là giao điểm của và đường thẳng . Tọa độ H là nghiệm của hệ
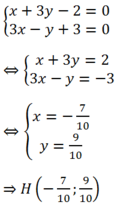
+Ta có H là trung điểm của MM’. Từ đó suy ra tọa độ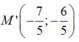 
Viết phương trình đường thẳng d’đi qua 2 điểm A và M’: điểm đi qua A( -1 ;1) , vectơ chỉ phương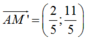 
=> vectơ pháp tuyến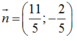 
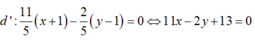
vẽ mặt phẳng tọa độ :
hàm số y=2x +4
cho x=0 \(\Rightarrow y=4\) \(\Rightarrow\) B(0, 4)
cho y=0 \(\Rightarrow x=-2\) \(\Rightarrow C\left(-2,0\right)\)
hàm số y= -x +3
cho \(x=0\Rightarrow y=3\Rightarrow D\left(0,3\right)\)
cho\(y=0\Rightarrow x=3\Rightarrow H\left(3,0\right)\)
Vẽ đường thẳng đi qua 2 điểm B và C ta được đồ thị hàm số y=2x+4
Vẽ đường thẳng đi qua 2 điểm D và H ta được đồ thị hàm số y=-x+3
do A thuộc đường thẳng (d) và (d') nên ta có phương trinh hoành độ giao điểm :
2x+4=-x+3
\(\Leftrightarrow3x=-1\Leftrightarrow x=\dfrac{-1}{3}\) \(\Rightarrow y=\dfrac{10}{3}\)
\(\Rightarrow A\left(\dfrac{-1}{3},\dfrac{10}{3}\right)\)