Số giá trị nguyên âm của m để \(m.9^x-\left(2m+1\right).6^x+m.4^x\ge0\forall x\in\left[0;1\right]\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-x^2-2\left(m-1\right)x+2m-1>0,\forall x\left(0;1\right)\)
\(\Leftrightarrow-2m\left(x-1\right)>x^2-2x+1,\forall x\in\left(0;1\right)\) (*)
Vì \(x\in\left(0;1\right)\Rightarrow x-1< 0\) nên (*) \(\Leftrightarrow-2m< \dfrac{x^2-2x+1}{x-1}=x-1=g\left(x\right),\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-2m\le g\left(0\right)=-1\Leftrightarrow m\ge\dfrac{1}{2}\)

\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)
Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất
\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)
\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)
\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)
\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)
\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)
Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:

Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)
\(\Rightarrow\) Có 6 giá trị nguyên của m

TH1: \(m=3\Rightarrow f\left(x\right)=-5< 0\) với mọi x(ktm)
TH2: \(m>3\Rightarrow f\left(x\right)\) đồng biến trên R
\(\Rightarrow\min\limits_{\left[3;4\right]}f\left(x\right)=f\left(3\right)=3\left(m-3\right)-2m+1=m-8\)
\(m-8>0\Rightarrow m>8\)
TH3: \(m< 3\Rightarrow f\left(x\right)\) nghịch biến trên R
\(\Rightarrow\min\limits_{\left[3;4\right]}=f\left(4\right)=4\left(m-3\right)-2m+1=2m-11\)
\(2m-11>0\Rightarrow m>\dfrac{11}{2}\) (ktm điều kiện \(m< 3\))
Kết hợp lại ta được \(m>8\)

Ta có: \(VT_{bpt}=m^2\left(x^4-1\right)+m\left(x^2-1\right)-6\left(x-1\right)\)(*)
\(=\left(x-1\right)\left[m^2\left(x+1\right)\left(x^2+1\right)+m\left(x+1\right)-6\right]\)
Ta xét \(f\left(x\right)=m^2\left(x+1\right)\left(x^2+1\right)+m\left(x+1\right)-6\)
+) m=0, rõ ràng không thỏa mãn
+) \(m\ne0\), thì f(x) là hàm số bậc 3, luôn có ít nhất 1 nghiệm, và luôn có lẻ số nghiệm(nghĩa là chỉ có 1 hoặc 3 nghiệm). Gọi nghiệm đó là \(x_o\) thì
\(f\left(x\right)=\left(x-x_o\right)\left(m^2x^2+bx+c\right)\)
Th1: \(ax^2+bx+c=\left(x-x_1\right)\left(x-x_2\right)\). Lúc này dấu của (*) đổi dấu trên từng khoảng, nên Th này loại.
Th2:\(ax^2+bx+c>0\forall x\) thì ta sẽ xét dấu của \(\left(x-1\right)\left(x-x_o\right)\). Biện luận tương tự Th1, để Bpt đúng với mọi x thì \(x_o=1\). Do đó f(x) phải nhận \(x_o\) làm nghiệm. Thay x=1 vào f(x):
\(m^2.4+2m-6=0\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-\dfrac{3}{2}\end{matrix}\right.\)
Thử lại thấy cả 2 giá trị của m đều thỏa mãn. Vậy \(S=-\dfrac{3}{2}+1=-\dfrac{1}{2}\)

\(m^2\left(x-1\right)+x-3< 0\Leftrightarrow\left(m^2+1\right)x-m^2-3< 0\)
Đặt \(f\left(x\right)=\left(m^2+1\right)x-m^2-3\)
\(f\left(x\right)< 0\forall x\in\left[-5;2\right]\Leftrightarrow\hept{\begin{cases}f\left(-5\right)< 0\\f\left(2\right)< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}-6m^2-8< 0\\m^2-1< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}6m^2+8>0\\m^2< 1\end{cases}}\Leftrightarrow\left|m\right|< 1\Leftrightarrow-1< m< 1\)
Vậy có duy nhất 1 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán, đó là giá trị m = 0

đi từ hướng làm để ra được bài toán:
Ta thấy muốn f(|x|) có 5 điểm cực trị thì f'(x) phải có 2 điểm cực trị dương
giải f'(x)=0 \(\left\{{}\begin{matrix}x=1\\x^2-2\left(m+1\right)x+m^2-1=0\left(2\right)\end{matrix}\right.\) phương trình (2) phải có 2 nghiệm phân biệt trái dấu nhau
Ta có: \(\Delta>0\Leftrightarrow m>-1\)
Theo yêu cầu bài toán: \(m^2-1>0\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>1\end{matrix}\right.\)
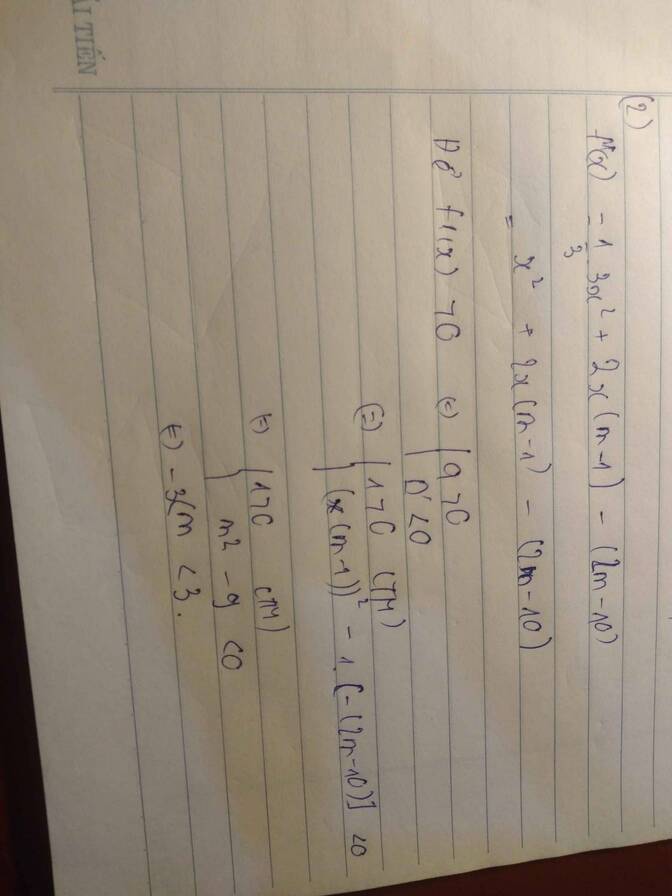
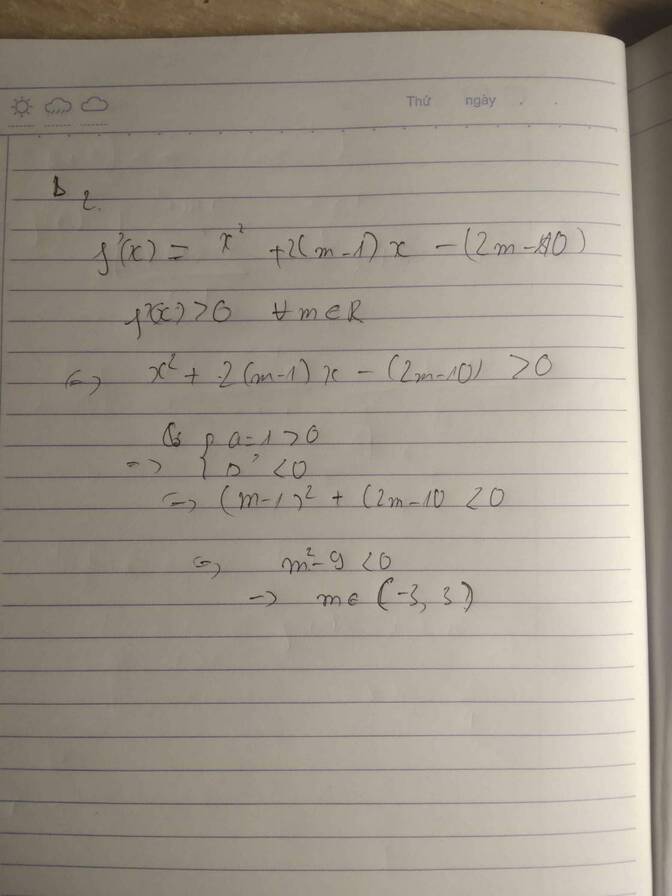

Lời giải:
Ta có \(m.9^x-(2m+1).6^x+m.4^x\geq 0\)
\(\Leftrightarrow m\left(\frac{9}{4}\right)^x-(2m+1)\frac{6^x}{4^x}+m\geq 0\)
\(\Leftrightarrow m[\left(\frac{3}{2}\right)^x]^2-(2m+1)\left(\frac{3}{2}\right)^x+m\geq 0\)
Đặt \(\left(\frac{3}{2}\right)^x=t; x\in [0;1]\Rightarrow t\in [1; \frac{3}{2}]\)
BPT trở thành: \(mt^2-(2m+1)t+m\geq 0\)
\(\Leftrightarrow m(t^2-2t+1)-t\geq 0\)
\(\Leftrightarrow m(t-1)^2-t\geq 0\) (*)với mọi \(t\in [1; \frac{3}{2}]\)
Nếu \(m\) là số nguyên âm, \(\Rightarrow m(t-1)^2\leq 0\)
\(t\in [1; \frac{3}{2}]\Rightarrow -t < 0\)
Do đó \(m(t-1)^2-t< 0\) (trái với (*)). Vậy có nghĩa là không tồn tại số nguyên âm m nào thỏa mãn điều kiện đã cho
Vậy có 0 giá trị thỏa mãn.