Cho tam giác ABC. Từ B vẽ cung tròn có bán kính AC và từ C vẽ cung tròn có bán kính AB, hai cung trnf này cắt hau tại D ( D và A khác phía nhau đối với BC )
a) C/M: tam giác BDC= tam giác CABvà góc ABD= góc DCA
b) Gọi M, N lần lượt là trung điểm của BD, AC. C/M: tam giác ABM= tam giác DCN và AM=DN
c) C/M: AM song song với DN

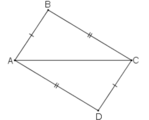
a) Xét Δ BDC và Δ CAB có:
BD = AC ( = R )
DC=AB(=R)
BC chung
\(\Rightarrow\) Δ BDC = Δ CAB( c.c.c)
\(\Rightarrow\)\(\widehat{ABD}\)=\(\widehat{DCA}\)( Hai góc tương ứng)
b)ΔBDC = Δ CAB
\(\Rightarrow\) BM=CN;DM=AN( Hai canh tương ứng)
Xét Δ ABM và ΔDCN có:
BM=CN(cmt)
\(\widehat{ABD}\)=\(\widehat{DCA}\)
AB=CD(=R)
\(\Rightarrow\)ΔABM=ΔDCN(c.g.c)
\(\Rightarrow\)AM=DN(Hai cạnh tương ứng)
c) AM=DN \(\Rightarrow\) AM // DN