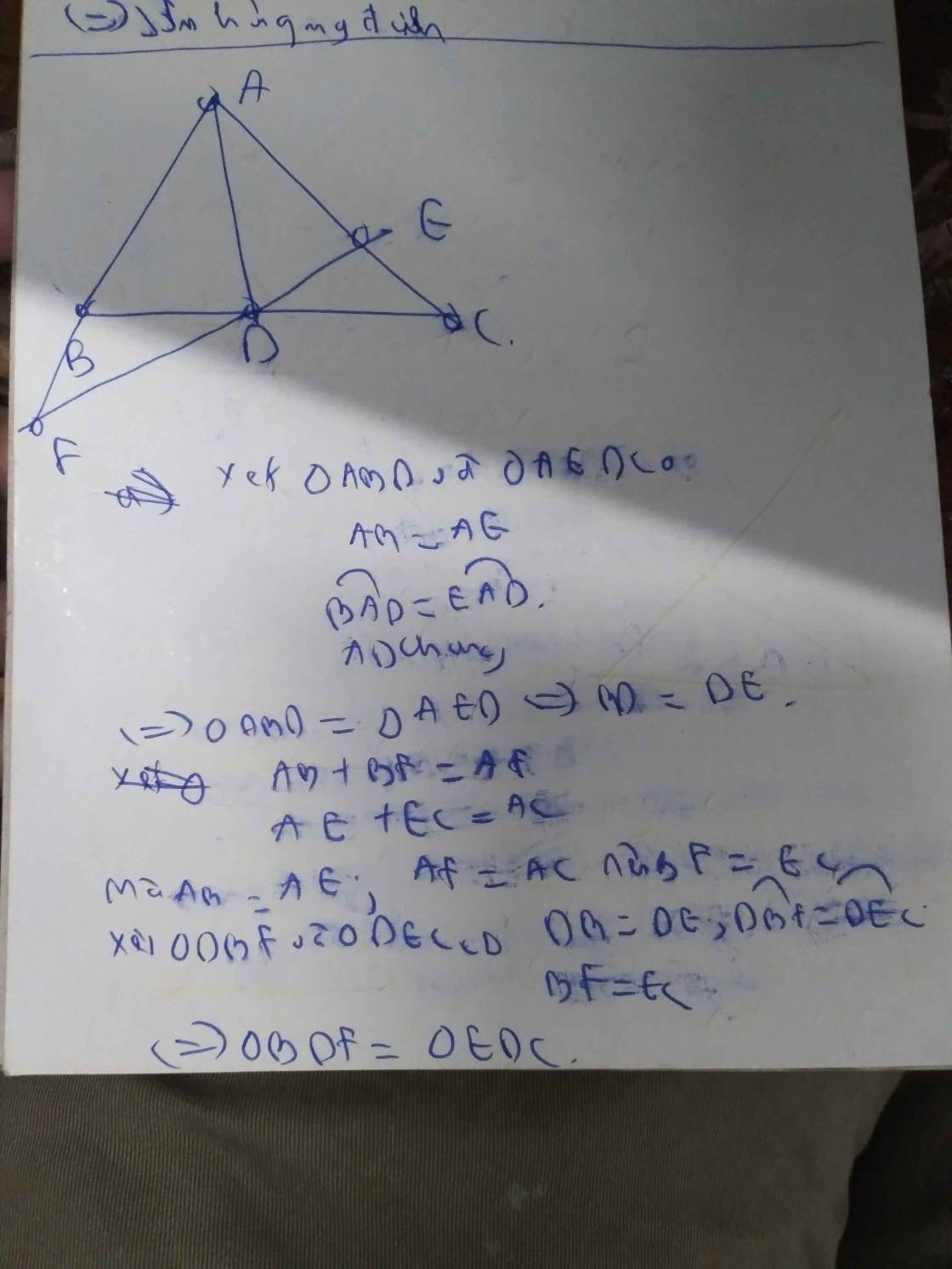
Cho tam giác ABC có AB < AC . Kẻ tia phân giác AD của góc BAC ( D thuộc BC ). Trên cạnh AC lấy điểm E sao cho AE = AB , trên tia AB lấy điểm F sao cho AF = AC . Chứng minh rằng :
a. \(\Delta BDF=\Delta EDC\) b. BF = EC
c. F,D,E thẳng hàng d. AD vuông góc FC


Lời giải:
a) Ta có:
\(\left\{\begin{matrix} AB=AE\\ AF=AC\end{matrix}\right.\Rightarrow AF-AB=AC-AE\)
\(\Leftrightarrow BF=CE\) (1)
Xét tam giác $ADF$ và $ADC$ có:
\(\left\{\begin{matrix} AD -\text{chung}\\ \angle FAD=\angle CAD(\text{do AD là phân giác})\\ AF=AC\end{matrix}\right.\)
\(\Rightarrow \triangle ADF=\triangle ADC(c.g.c)\Rightarrow DF=DC\) (2)
Tương tự, ta cm đc \(\triangle ABD=\triangle AED(c.g.c)\Rightarrow BD=ED\) (3)
Từ \((1);(2);(3)\Rightarrow \triangle BDF=\triangle EDC\) (c.c.c)
b) Đã chứng minh ở phần a
c) Vì \(\triangle BDF=\triangle EDC(cmt)\Rightarrow \angle BDF=\angle EDC\)
\(\Rightarrow \angle BDF+\angle BDE=\angle EDC+\angle BDE\)
\(\Leftrightarrow \angle FDE=\angle BDC=180^0\Rightarrow F,D,E\) thẳng hàng
d)
Do $AF=AC$ nên tam giác $FAC$ cân tại $A$. Do đó đường phân giác $AD$ đồng thời cũng là đường cao ứng với cạnh đáy $FC$ (tính chất của tam giác cân)
\(\Rightarrow AD\perp FC\) (đpcm)