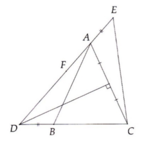
Cho △ABC,đường trung trực d của cạnh AB cắt tia BC tại D trên tia Ad lấy AE=BC a)chứng minh ΔABC=ΔBAE b)chứng minh AB//CE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét \(\Delta\)ADB có DM là trung tuyến đồng thời là đường cao
=> \(\Delta\)ADB cân tại D
=> \(\widehat{BAD}=\widehat{ABD}\)hay \(\widehat{BAE}=\widehat{ABC}\)
Xét \(\Delta ABC\)và \(\Delta BAE\)có:
AB chung
\(\widehat{ABC}=\widehat{BAE}\left(cmt\right)\)
BC=AE
=> \(\Delta ABC=\Delta BAE\left(cgc\right)\)

Rõ ràng góc ABC>90 ,trung trực AB ko cắt tia BC mà cắt tia đối của tia BC(trái gt),nếu góc ABC=90=>trung trực AB//BC,vậy theo bài ra góc ABC<90, xét 2 trường hợp :
1)góc ABC<góc BAC=>trung trực AB cắt đoạn BC tại D
a) Xét ..........
AB chung
tam giác ADB cân tại D=>góc DAB=góc DBA
AE=BC(gt)
=>tam giác BAE=tam giácABC
b) DC=BC-BD=AE-AD=DE
=>tam giác DEC cân tại D
=>góc DCE= góc ADC/2=gócABC
=>AB//CE(cac goc o vi tri so le trong=nhau)
2)gócABC>gócBAC=>trung trực AB cắt tia BC kéo dài
a)c/m như trên
b)DC=DB-BC=DA-AE=ED=>tam giác EDC cân tại D
=>góc ECD=góc ABC(cac goc o vi tri dong vi)
=> AB//CE ( đpcm )

b:
Vì D nằm trên đường trung trực của AB
nên DA=DB
=>DC=DE
Xét ΔDAB và ΔDEC có
DA/DE=DB/DC
góc ADB=góc EDC
Do đó: ΔDAB đồng dạng với ΔDEC
=>góc DAB=góc DEC
=>AB//EC

a: Xét ΔABC và ΔBAE có
AB chung
\(\widehat{ABC}=\widehat{BAE}\)
BC=AE
Do đó: ΔABC=ΔBAE
b: Xét ΔCDE và ΔBDA có
\(\widehat{CDE}=\widehat{BDA}\)
DC/DB=DE/DA
Do đó: ΔCDE\(\sim\)ΔBDA
Suy ra: \(\widehat{DCE}=\widehat{DBA}\)
=>CE//AB