Giải phương trình hộ em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có : G - T = 140 nu
2T + 3G = 2520
=> A = T = 420 nu
G = X = 560 nu
N = 2 ( A + G ) = 1960 nu
l = N x 3,4 : 2 = 3332Ao
Ta có: \(G-T=140\)
\(2T+3G=2520\)
\(\Rightarrow\left\{{}\begin{matrix}A=T=420nu\\G=X=560nu\end{matrix}\right.\)
\(N=2A+2G=2\cdot420+2\cdot560=1960nu\)
\(l=\dfrac{2N}{3,4}=\dfrac{2\cdot1960}{3,4}=1152,94A^o\)



Điều kiện xác định :
\(\left\{{}\begin{matrix}2x-2\ne0\\x-1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\ne2\\x\ne1\end{matrix}\right.\)
\(\Leftrightarrow x\ne1\)
\(\dfrac{2x+1}{2x-2}=\dfrac{2}{x-1}\)
\(\Leftrightarrow\dfrac{2x+1}{2x-2}-\dfrac{2}{x-1}=0\)
\(\Leftrightarrow\dfrac{2x+1}{2\left(x-1\right)}-\dfrac{2}{x-1}=0\)
\(\Leftrightarrow\dfrac{2x+1-2.2}{2\left(x-1\right)}=0\)
\(\Leftrightarrow2x+1-4=0\)
\(\Leftrightarrow2x-3=0\)
\(\Leftrightarrow x=\dfrac{3}{2}\left(tmdk\right)\)
Vậy \(S=\left\{\dfrac{3}{2}\right\}\)

\(\left(x-1\right)^3+x^3+\left(x+1\right)^3=\left(x+2\right)^3\)
\(\Leftrightarrow x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1-x^3-6x^2-12x-8=0\)
\(\Leftrightarrow2x^3-6x^2-6x-8=0\)
\(\Leftrightarrow2.\left(x^3-3x^2-3x-4\right)=0\)
\(\Leftrightarrow x^3-4x^2+x^2-4x+x-4=0\)
\(\Leftrightarrow x^2.\left(x-4\right)+x.\left(x-4\right)+\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right).\left(x^2+x+1\right)=0\)
Mà \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
\(\Rightarrow x-4=0\Leftrightarrow x=4\)


a: =>x^2+5x-6>=0
=>(x+6)(x-1)>=0
=>x>=1 hoặc x<=-6
b: -5x^2+12x+6>0
=>5x^2-12x-6<0
=>\(\dfrac{6-\sqrt{66}}{5}< x< \dfrac{6+\sqrt{66}}{5}\)
c: =>7x^2-8x-12>=0
=>7x^2-14x+6x-12>=0
=>(x-2)(7x+6)>=0
=>x>=2 hoặc x<=-6/7
d: =>(x+2)(x+3)>=0
=>x>=-2 hoặc x<=-3


 mọi ng giải hộ em bài này với ạ( có lập bảng và giải bằng hệ phương trình ạ) e cần gấp
mọi ng giải hộ em bài này với ạ( có lập bảng và giải bằng hệ phương trình ạ) e cần gấp mọi người lập bảng giải hộ em bằng hệ phương trình với ạ. E cần gấp, em cảm ơn
mọi người lập bảng giải hộ em bằng hệ phương trình với ạ. E cần gấp, em cảm ơn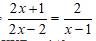
 giải hộ mình với ạ. xin cảm ơn
giải hộ mình với ạ. xin cảm ơn

\(3x^2-2x+5=0\)
\(\Leftrightarrow2x^2+x^2-2x+1+4=0\)
\(\Leftrightarrow2x^2+\left(x-1\right)^2=-4\)
Phương trình vô nghiệm.
Sai đề phải là 3x2-2x-5=0
Ta có:3x2-2x-5=0
<=> 3x2+3x-5x-5=0
<=> 3x(x+1)-5(x+1)=0
<=> (x+1)(3x-5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{5}{3}\end{matrix}\right.\)