Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Hàm bậc 4 trùng phương có ba điểm cực trị ⇒ a b < 0 ⇒ 9 m − 4 < 0 ⇔ m − 4 < 0 ⇔ m < 4
Áp dụng công thức giải nhanh ba điểm cực trị tạo thành tam giác đều thì:
24 a + b 3 = 0 ⇔ 24.9 + m − 4 3 = 0 ⇔ m = − 2
Vậy giá trị m 0 gần giá trị -1 nhất

Chọn A
![]()
Đồ thị hàm số có điểm cực trị là A(1;3), ta có
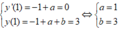
Khi đó ta có, 4a-b=1.

Chọn C.
Đặt f x = e 2 x a cos 3 x + b sin 3 x + c
Ta có f ' x = 2 a + 3 b e 2 x cos 3 x + 2 b - 3 a e 2 x sin 3 x
Để f(x) là một nguyên hàm của hàm số e 2 x cos 3 x , điều kiện là
f ' ( x ) = e 2 x cos 3 x ⇔ 2 a + 3 b = 1 2 b - 3 a = 0 ⇔ a = 2 13 b = 3 13 ⇒ a + b = 5 13

\(4\left(x-8\right)< 0\)
\(\Rightarrow x-8< 0\)
\(\Rightarrow x< 8\)
mà x thuộc N
\(\Rightarrow x\in\left\{0;1;2;...;6;7\right\}\)

theo bài ra ta có: | a+7 | + | b-3 | = 0
=> a+7=0 và b-3 = 0
với a+7 =0 => a= 0-7 = -7
với b-3 = 0 => b= 3+0 =3
vậy a+b = -7 + 3 = -4
vậy a+b có giá trị bằng -4
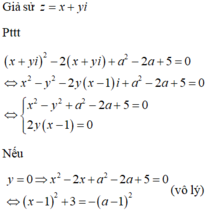
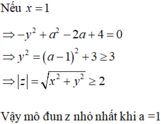


\(x^2+y^2+z^2+2x-4y+6z=-14\\ x^2+2x+1+y^2-4y+4+z^2+6z+9=0\\ \left(x+1\right)^2+\left(y-4\right)^2+\left(z+3\right)^2=0\\ \Rightarrow\left\{{}\begin{matrix}x+1=0\\y-4=0\\z+3=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-1\\y=4\\z=-3\end{matrix}\right.\\ \Rightarrow x+y+z=-1+4-3=0\)
có \(x^2+y^2+z^2+2x-4y+6z=-14\)
=>\(x^2+z^2+y^2+2x-4y+6z+14=0\)
=>\(\left(x^2+2x+1\right)+\left(y^2-4y+4\right)+\left(z^2+6y+9\right)=0\)
=>\(\left(x+1\right)^2+\left(y-2\right)^2+\left(z+3\right)^2=0\)
=> x+1 =0
y-2 =0
z+3 =0
=> x = -1
y = 2
z = -3
=> x + y + z = -2