Cho hình bình hành ABCD, O là giao điểm hai đường chéo AC và BD. Gọi M, N lần lượt là trung điểm của OB, OD.
a) Chứng minh: Tứ giác AMCN là hình bình hành.
b) Tia AM cắt BC ở E, tia CN cắt AD ở F. Chứng minh: Ba đường thẳng AC,BD, EF đồng quy.
c) Chứng minh: BE = \(\dfrac{1}{2}EC\)
Mk làm được phần a) và b) rùi mà phần c) nghĩ mãi hông ra à! T^Thic hic M.n giúp mk nha... CẢM ƠN M.N NHÌU !!!!!

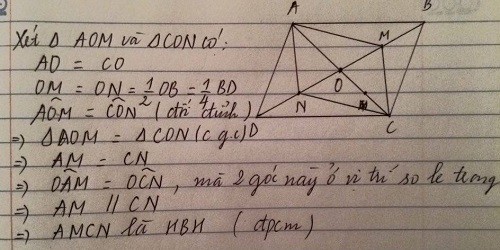
a: Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(1)
=>O là trung điểm chung của AC và BD
Xét tứ giác AMCN có
O là trung điểm của AC
O là trung điểm của MN
Do đó: AMCN là hìnhbình hành
b: Xét tứ giác AFCE có
AF//CE
AE//CF
Do đó: AFCE là hình bình hành
Suy ra: Hai đường chéo AC và FE cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,BD,FE đồng quy
c: Gọi K là trung điểm của CE
Xét ΔCAE có
K là trung điểm của CE
O là trung điểm của AC
Do đó: KO là đường trung bình
=>KO//AE
hay EM//OK
Xét ΔBOK có
M là trung điểm của OB
ME//OK
Do đó: E là trung điểm của BK
=>BE=EK=KC
=>BE=1/2EC