Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì ABCD là hình thoi(gt). Mà AC và BD cắt nhau tại O
=> O là trung điểm của AC và BD (t/c của hình bình hành)
=> OB=OD. Mà BE=DF(gt)
=> OB-BE=OD-DF => OE=OF. Mà O nằm giữa E và F
=> O là trung điểm của EF
Xét tứ giác AECF có: AC cắt EF tại O
Mà O là trung điểm của AC( c/m trên )
O là trung điểm của EF( c/m trên )
=> AECF là hình bình hành (Tứ giác có 2 đ/c cắt nhau tại trung điểm của mỗi đg là hình bình hành)
b) Để AECF là hình thoi => \(AC\perp EF\) tại O
=> \(AC\perp BD\) tại O \(\left(E,F\in\left(O\right)\right)\)
Xét hình bình hành ABCD có: \(AC\perp BD\) tại O (c/m trên)
=> ABCD là hình thoi (Hình bình hành có 2 đ/c vuông góc là hình thoi)
Vậy để AECF là hình thoi thì ABCD là hình thoi
a) Vì ABCD là hình thoi(gt). Mà AC và BD cắt nhau tại O
=> O là trung điểm của AC và BD (t/c của hình bình hành)
=> OB=OD. Mà BE=DF(gt)
=> OB-BE=OD-DF => OE=OF. Mà O nằm giữa E và F
=> O là trung điểm của EF
Xét tứ giác AECF có: AC cắt EF tại O
Mà O là trung điểm của AC( c/m trên )
O là trung điểm của EF( c/m trên )
=> AECF là hình bình hành (Tứ giác có 2 đ/c cắt nhau tại trung điểm của mỗi đg là hình bình hành)
b) Để AECF là hình thoi => AC⊥EFAC⊥EF tại O
=> AC⊥BD tại O (E,F∈(O)
Xét hình bình hành ABCD có: AC⊥BDAC⊥BD tại O (c/m trên)
=> ABCD là hình thoi (Hình bình hành có 2 đ/c vuông góc là hình thoi)
Vậy để AECF là hình thoi thì ABCD là hình thoi

a: Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(1)
=>O là trung điểm chung của AC và BD
Xét tứ giác AMCN có
O là trung điểm của AC
O là trung điểm của MN
Do đó: AMCN là hìnhbình hành
b: Xét tứ giác AFCE có
AF//CE
AE//CF
Do đó: AFCE là hình bình hành
Suy ra: Hai đường chéo AC và FE cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,BD,FE đồng quy
c: Gọi K là trung điểm của CE
Xét ΔCAE có
K là trung điểm của CE
O là trung điểm của AC
Do đó: KO là đường trung bình
=>KO//AE
hay EM//OK
Xét ΔBOK có
M là trung điểm của OB
ME//OK
Do đó: E là trung điểm của BK
=>BE=EK=KC
=>BE=1/2EC

a) Tứ giác ABCD có O là giao điểm của AC và BD
=> OA = OC;
và OB = OD (1)
M là trung điểm OB => OM = 1/2 OB (2)
N là trung điểm OD => ON = 1/2 OD (3)
Từ (1), (2) và (3) suy ra: OM = ON
Tứ giác AMCN có: OA = OC; OM = ON
suy ra: AMCN là hình bình hành
b) Tứ giác AECF có: AE // CF; AF // CE
=> AECF là hình bình hành
mà O là trung điểm AC
=> AC và EF giao tại O
Vậy AC, BD, EF đồng quy tại O

a) ABCD là hình bình hành có O là giao AC và BD
=> OA=OC; OB = OD
M, N lần lượt là trung điểm OB,OD => OM = 1/2 OB; ON = 1/2 OD
suy ra:OM = ON
Tứ giác AMCN có OA=OC; OM = ON
=> AMCN là hình bình hành
b) Tứ giác AECF có: AE // CF; AF // CE
=> AECF là hình bình hành
mà O là trung điểm AC
=> AC và EF giao tại O
Vậy AC, BD, EF đồng quy tại O
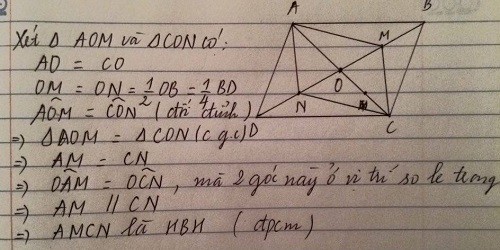
AMCN la hình bình hành vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường.
AECF là hình bình hành vì AM song song AN nên AE song song CF, AD song song BC nên AF song song EC.
Suy ra AC và EF cắt nhau tại trung điểm của mỗi đường mà AC và BD cũng cắt nhau tại trung điểm của mỗi đường.
Nên AC, BD, EF đồng quy.
Tam giác BCM có NE song song CM vì AE song song CF, suy ra BN/NM=BE/EC=1/2 suy ra ĐIỀU PHẢI CHỨNG MINH ^_^