Bài 5.5 ạ!
Bài 5.5 ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TX
4
LD
19 tháng 4 2022
Một xe máy đi với vận tốc 50 km/giờ. Hỏi xe máy đó đi hết quãng đường 112,5 km trong bao lâu?
19 tháng 4 2022
\(\dfrac{3}{4}.\dfrac{4}{5}.\dfrac{5}{6}.....\dfrac{99}{100 }\) Giải: \(=\dfrac{3}{1.4}.\dfrac{4}{1.5}.\dfrac{5}{1.6}...\dfrac{99}{1.100}\)
\(=\dfrac{4-1}{1.4}.\dfrac{5-1}{1.5}.\dfrac{6-1}{1.6}...\dfrac{100-1}{1.100}\)
\(=1-\dfrac{1}{4}.1-\dfrac{1}{5}.1-\dfrac{1}{6}...1-\dfrac{1}{100}\)
\(=1\left(\dfrac{1}{4}-\dfrac{1}{5}-\dfrac{1}{6}-...-\dfrac{1}{100}\right)\)
PL
3
Làm giúp mk ý c bài 5.5
26 tháng 1 2023
5.5:
a: Vì (d)//y=1/2x-1 nên a=1/2
=>y=1/2x+b
Thay x=0 và y=2 vào (d), ta được;
b+1/2*0=2
=>b=2
=>(d): y=1/2x+2
b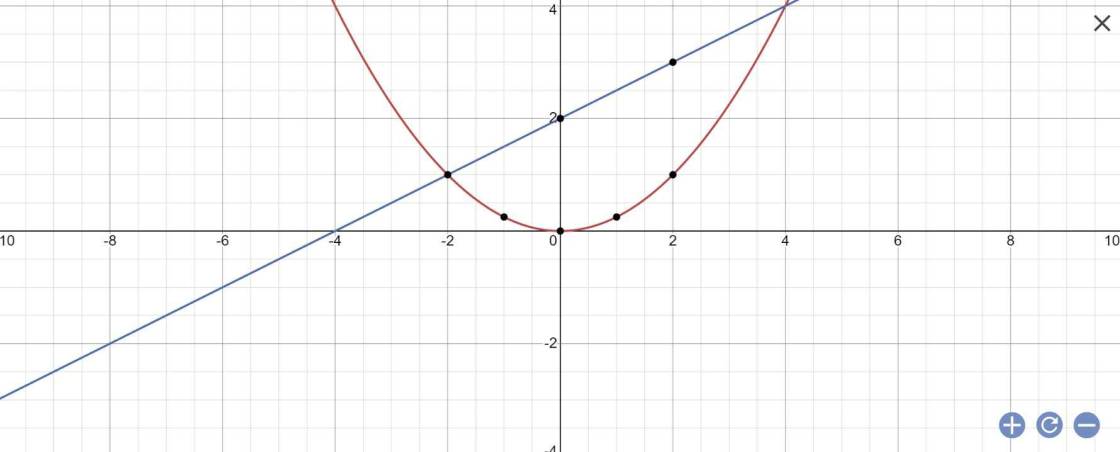 
c: PTHDGĐ là:
1/4x^2=1/2x+2
=>1/4x^2-1/2x-2=0
=>x^2-2x-8=0
=>(x-4)(x+2)=0
=>x=4 hoặc x=-2
Khi x=4 thì y=1/4*x^2=1/4*4^2=4
Khi x=-2 thì y=1/4*(-2)^2=1
=>A(4;4); B(-2;1)
\(OA=\sqrt{4^2+4^2}=4\sqrt{2}\)
\(OB=\sqrt{\left(-2\right)^2+1^2}=\sqrt{5}\)
\(AB=\sqrt{\left(-2-4\right)^2+\left(1-4\right)^2}=3\sqrt{5}\)
\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=-\dfrac{\sqrt{10}}{10}\)
=>\(sinAOB=\dfrac{3\sqrt{10}}{10}\)
\(S_{OAB}=\dfrac{1}{2}\cdot4\sqrt{2}\cdot\sqrt{5}\cdot\dfrac{3}{\sqrt{10}}=2\cdot3=6\)
ND
1
CC
23 tháng 5 2021
Câu 5.5 trang 16 Sách Bài Tập SBT Toán lớp 7 tập 1
Tính:
M = 22010 - (22009 + 22008 + ... + 21 + 20)
Giải
Đặt A = 22009 + 22008 + ... + 21 + 20
Ta có 2A = 22010 + 22009 + ... + 22 + 21.
Suy ra 2A - A = 22010 - 20 = 22010 - 1.
Do đó M = 22010 - A = 22010 - (22010 - 1) = 1.
B52
TC
2
29 tháng 7 2017
bạn ơi 0 có bài 5.5 đâu. năm nay mình lên lớp 7 nè. chả thấy bài nào
TH
4
TH
2 tháng 10 2021
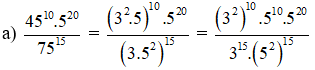
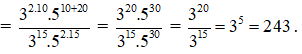
GIÚP MÌNH VỚI MN ƠIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
2 tháng 10 2021
\(A=\dfrac{\left(20.5\right)^5.5^5}{100^5}=\dfrac{100^5.3125}{100^5}=3125\)
\(B=\dfrac{\left(0,3.3\right)^5}{\left(0,3\right)^5.0,3}=\dfrac{\left(0,3\right)^5.3^5}{\left(0,3\right)^5.0,3}=\dfrac{3^5}{0,3}=810\)
5 tháng 8 2018
E=1.1+2.2+3.3+...+50.50
E= 1. ( 2-1) + 2. (3-1)+..+50.(51-1)
E=1.2-1.1+2.3-2.1+...+50.51-50.1
E=(1.2+2.3+...+50.51)-(1.1+2.1+...+50.1)
đặt là A đặt là B
xét A=1.2+2.3+...+50.51
3A=1.2.3+2.3.3+...+50.51.3
=1.2.3+2.3.4-1.2.3+..+50.51.52-49.50.51
=50.51.52
=132600
xét B= 1.1+1.2+...+50.1
B=1+2+3+...+50
số số hạng của A chính bằng số số hạng của dãy số tự nhiên liên tiếp cách đều 1 đơn vị từ 1 đến 50
số số hạng của A là 50:1+1=50 ( số hạng )
tổng A là (50+1).50:2=1275
thay vào E ta có
E=132600-1275
E=11925
vậy E=11925
đúng thì k
N
1
LM
15 tháng 11 2016
\(\frac{2^5.7+2^5.59}{2^5.5^2-2^5.3}\)
=\(\frac{\left(2^5\right).\left(7+59\right)}{\left(2^5\right).\left(5^2-3\right)}\)
=\(\frac{7+59}{5^2-3}\)
=\(\frac{64}{22}\)
=\(\frac{32}{11}\)
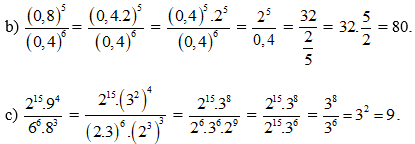
a;Zn + 2HCl\(\rightarrow\)ZnCl2+H2
Zn+ H2SO4\(\rightarrow\)ZnSO4+H2
b;TN1:
\(\sum n_{H_2}=0,1+0,1=0,2\left(mol\right)\)
VH2=22,4.0,2=4,48(lít)
TN2:
\(\sum n_{H_2}=0,1+0,05=0,15\left(mol\right)\)
VH2=22,4.0,15=3,36(lít)
Vậy ở TN1 sinh ra nhiều H2 hơn