Trong trường hợp ba suất điện động của máy phát ba pha mắc theo hình sao và ba tải cũng được mắc theo hình sao thì phải có bốn đường dây nối từ nguồn đến tải. Hãy xét trường hợp ba tải đối xứng và chứng minh rằng trong số bốn đường dây nối ấy có một đường dây tại đó cường độ dòng điện luôn bằng 0 (đường dây trung hòa).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Khi các suất điện động và tải đối xúng đều mắc hình sao thì dòng điện trong các tải có cùng biên độ, tần số, và các dòng đôi một lệch pha nhau góc 2π/3.
+ Biểu thức cường độ dòng điện trong các tải là:
i1 = I0.cosωt; i2 = I0.cos(ωt - 2π/3); i3 = I0.cos(ωt + 2π/3)
→ cường độ dòng điện trong dây trung hòa là:
i = i1 + i2 + i3 = I0.cosωt+ I0.cos(ωt - 2π/3) + I0.cos(ωt + 2π/3)
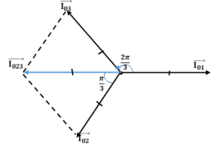
Cộng ba hàm điều hòa trên bằng giãn đồ vectơ.
Ta thấy 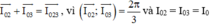
nên I023 = I0 = I01 và 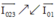
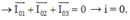

Chọn đáp án C
i th = i 1 + i 2 + i 3 = 220 2 10 + 220 2 ∠ 2 π 3 3 + 220 2 ∠ - 2 π 3 20 i = 33 6 ⇒ i th = 33 6 cos 100 π t ( A )

Chọn đáp án A
i th = i 1 + i 2 + i 3 = 3 + 2 ∠ - 2 π 3 + 2 ∠ 2 π 3 = 1 ⇒ i th = cos 100 π t ( A )

Chọn đáp án C
Z L = ω L = 16 ( Ω ) ⇒ Z = R 2 + Z L 2 = 20 ( Ω ) I 1 = I 2 = I 3 = U R = U p 3 R ⇒ P = 3 I 1 2 R = 4356 ( W )

Chọn đáp án B
Vì tải đối xứng nên dòng điện qua dây trung hòa bằng 0.
I 1 = I 2 = I 3 = U R = U p R = 2 , 9 ( A )
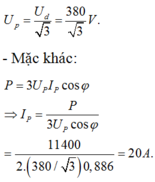
Vì ba tải đối xứng nên ba vecto quay của ba dòng điện trong các tải đó có dạng như hình 17.2. Dòng điện qua dây trung hòa là tổng của ba dòng điện qua ba tải.
Do tính đối xứng ta có :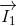 +
+ 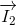 +
+ 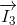 =
= 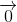 .
.
Vậy dòng điện qua dây trung hòa bằng 0.