\(x^3+6x^2-13x-42\)
Rút gọn biểu thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1/
a/ \(D=2x\left(10x^2-5x-2\right)-5x\left(4x^2-2x-1\right)\)
\(D=2x\left[10\left(x^2-\frac{1}{2}x-\frac{1}{5}\right)\right]-5x\left[4\left(x^2-\frac{1}{2}x-\frac{1}{4}\right)\right]\)
\(D=20x\left(x^2-\frac{1}{2}x-\frac{1}{5}\right)-20x\left(x^2-\frac{1}{2}x-\frac{1}{4}\right)\)
\(D=20x^3-10x^2-4x-20x^3+10x^2+5x\)
\(D=x\)
b/ Mình xin sửa lại đề:
Tính giá trị biểu thức \(E\left(x\right)=x^5-13x^4+13x^3-13x^2+13x+2012\)
Tại x = 12
\(E\left(x\right)=x^5-\left(x+1\right)x^4+\left(x+1\right)x^3-\left(x+1\right)x^2+\left(x-1\right)x+2012\)
\(E\left(x\right)=x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2-x+2012\)
\(E\left(x\right)=2012-x\)
\(E\left(x\right)=2000\)
2/
a/ \(2x\left(x-5\right)-x\left(3+2x\right)=26\)
<=> \(2x^2-10x-3x-2x^2=26\)
<=> \(-13x=26\)
<=> \(x=-2\)
b/ Bạn vui lòng coi lại đề.
3a/ Ta có \(D=x\left(5x-3\right)-x^2\left(x-1\right)+x\left(x^2-6x\right)-10+3x\)
\(D=5x^2-3x-x^3+x^2+x^3-6x^2-10+3x\)
\(D=-10\)
Vậy giá trị của D không phụ thuộc vào x (đpcm)

(x+1)\(^3\)-(x-1)\(^3\)-6x\(^2\)
=x\(^3\)+3x\(^2\)+3x+1-x\(^3\)+3x\(^2\)-3x+1-6x\(^2\)
=2

\(\left(x+2\right)^3-2\left(x^2+6x-5\right)-8\)
\(=x^3+6x^2+12x+8-2x^2-12x+10-8\)
\(=x^3+4x^2+10\)

\(a,\dfrac{x^2+6x+9}{x+3}\\ đk:x\ne-3\\ =\dfrac{\left(x+3\right)^2}{x+3}=x+3\)
b, Thay \(x=-2\left(t/mđk\right)\) vào
\(-2+3=1\)
Vậy tại \(x=-2\) thì biểu thức = 1
\(A=\dfrac{x^2+6x+9}{x+3}\)
\(A=\dfrac{x^2+2.x.3+3^2}{x+3}\)
\(A=\dfrac{\left(x+3\right)^2}{x+3}\)
\(A=x+3\)
b) Thay x = -2 vào A ta được A = -2 + 3 = 1
Vậy khi x = -2 thì A = 1
cho − 3 bé hơn bằng x bé hơn bằng 3 rút gọn biểu thức T= \(\sqrt{x^2-6x+9}+\sqrt{x^2+6x+9}\) ta được

Ta có: \(T=\sqrt{x^2-6x+9}+\sqrt{x^2+6x+9}\)
\(=\left|x-3\right|+\left|x+3\right|\)
\(=3-x+x+3\)
\(=6\)

1/2 x 2 (6x – 3) – x( x 2 + 1/2) + 1/2.(x + 4)
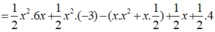
= (3 x 3 – 3/2. x 2 ) – ( x 3 + 1/2.x) + (1/2.x + 2)
= 3 x 3 - 3/2 x 2 – x 3 - 1/2 x + 1/2 x + 2
= ( 3 x 3 – x 3 ) - 3/2. x 2 – (1/2 x - 1/2 x) + 2
= 2 x 3 - 3/2 x 2 + 2
Chắc là phân tích đa thức thành nhân tử hả bạn?
\(x^3+6x^2-13x-42\)
\(=x^3+2x^2+4x^2+8x-21x-42\)
\(=x^2\left(x+2\right)+4x\left(x+2\right)-21\left(x+2\right)\)
\(=\left(x^2+4x-21\right)\left(x+2\right)\)
\(x^3+6x^2-13x-42\)
\(=x^3+2x^2+4x^2+8x-21x-42\)
\(=x^2\cdot\left(x+2\right)+4x\cdot\left(x+2\right)-21\left(x+2\right)\)
\(=\left(x+2\right)\cdot\left(x^2+4x-21\right)\)
\(=\left(x+2\right)\cdot\left(x^2+7x-3x-21\right)\)
\(=\left(x+2\right)\cdot\left(x\cdot\left(x+7\right)-3\left(x+7\right)\right)\)
\(=\left(x+2\right)\left(x-3\right)\left(x+7\right)\)