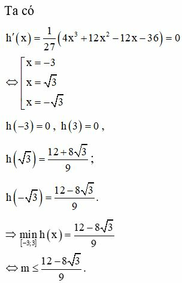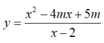Tìm tập hợp các điểm M có tọa độ như sau với mọi số thực m:
a) M (m ; -1)
b) M (2 ; m)
c) M (m ; m)
d) M (m; -m)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 3 2018
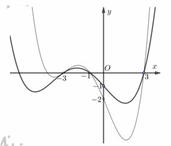
Đáp án D
Đồ thị hàm số ( C m ) có hai điểm phân biệt đối xứng nhau qua gốc tọa độ khi và chỉ khi tồn tại
13 tháng 1 2023
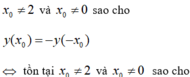
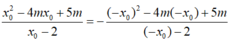
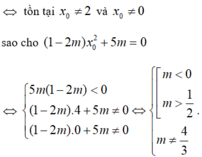
a: Gọi (d): y=ax+b là tập hợp các điểm M cần tìm
Thay x=m và y=-1 vào (d), ta được;
ma+b=-1
=>ma=-1-b
=>m=(-b-1)/a
b: Thay x=2 và y=m vào (d), ta được:
2a+b=m
=>m=2a+b
c: Thay x=m và y=m vào (d), ta được:
ma+b=m
=>m(a-1)=m
=>m=m/(a-1)
=>M nằmtrên đường y=x
d: Vì M(m;-m) nên M nằm trên đường y=-x
CM
13 tháng 5 2019
Đáp án là B.
• Trường hợp m = 0
f x = − x 2 + 1 có đồ thị là parabol, có đỉnh I(0;-1).
Đồ thị hàm số đã cho có một điểm cực đại là I thuộc trục tung.
Do đó m = 0 thoả yêu cầu bài toán.
• Trường hợp m ≠ 0
f ' x = 4 m x 3 − 2 m + 1 x
f ' x = 0 ⇔ x = 0 ∨ x 2 = m + 1 2 m
+ Nếu − 1 ≤ m < 0 thì f ' ( x ) = 0 có nghiệm x = 0 ( y = m + 1 )
Đồ thị hàm số có một điểm cực đại (0;m+1) thuộc trục toạ độ.
+ Nếu m < − 1 ∨ m > 0 thì f ' ( x ) = 0 có ba nghiệm phân biệt
x = 0 y = m + 1 x = m + 1 2 m ( y = 3 m 2 + 2 m − 1 4 m ) x = − m + 1 2 m ( y = 3 m 2 + 2 m − 1 4 m )
Khi đó đồ thị hàm số có các điểm cực trị thuộc các trục toạ độ khi và chỉ khi 3 m 2 + 2 m − 1 = 0 ⇔ m = − 1 ∨ m = 1 3 . Nhận m = 1 3
