a) Vẽ a // b và \(c\perp a\)
b) Quan sát xem c có vuông góc với b hay không ?
c) Lí luận tại sao nếu a // b và \(c\perp a\) thì \(c\perp b\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
2 tháng 8 2016
a)
b) Ta có:
Ta có c ⊥ b vì a // b nên nếu cắt a tại a thì c cũng cắt b tại b. Vì góc C1 = 90o nên góc B2 so le trong với nó cũng bẳng 900
Vây c ⊥ b.
C) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
a ⊥ c
a // b
=> c ⊥ b.
HT
15 tháng 7 2016
a,
a // b; c vuông góc với a tại M và cắt b tại N (như hình vẽ)
b, Theo quan sát chắc chắn c vuông góc với b
c, Lý luận:
Có a // b (gt)
c cắt a và b lần lượt tại M và N (hình vẽ)
=> Góc M1 = góc N2 (2 góc đồng vị)
Mà a vuông góc với c
=> góc M1 = 90o
=> góc N2 = 90o
=> b vuông góc với c
20 tháng 5 2022
b: c có vuông góc với b
c: Vì a//b thì ta sẽ có hai góc so le trong bằng nhau
mà c vuông góc với a nên sẽ có 1 trong hai góc so le trong đó bằng 90 độ
Từ đó dẫn tới góc so le trong còn lại giữa b và c bằng 90 độ
=>ĐPCM
11 tháng 10 2016
1
a) vẽ c ⊥ a.
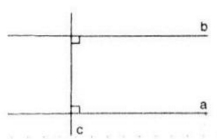
b) Vẽ như hình trên.
a song song với b do a và b đều vuông góc với c (Từ vuông góc đến song song)
2 a .Hình vẽ tương tự như câu 1.
B. b và c vuông góc với nhau do b // a mà a ⊥ c. (tính chất từ vuông góc đến song song)
3 a. câu này bn tự vẽ nhé
B. Giả sử b không song song với c thì b cắt c tại một điểm O nào đó. khi đó qua O ta có thể vẽ được hai đường thẳng b và c cùng song song với a. Điều đó trái với tiên để Ơclit về đường thẳng song song. Vậy b// c.
Tíck cho mk nha !
11 tháng 10 2016
1 )
a , b )
Vì c \(\perp\) a ( 1 )
c \(\perp\) b ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\) a // b
Ta có hình vẽ :
HN
30 tháng 6 2018
a, Nếu b//c và a \(\perp\)b thì a \(\perp\)c
b, Nếu a//b và c//a thì b // c
c, Nếu b \(\perp\)c và a \(\perp\)b thì a // c
d, Nếu AB //a và BC //a thì AB // BC
e, Hai tia phân giác của hai góc kề bù thì vuông góc với nhau
cs đứng k vậy bn