rút gọn biểu thức A = (tan2a - sin2a) / (cot2a - cos2a) là bao nhiêu ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(1+tan^2a\right)\left(1-sin^2a\right)-\left(1+cot^2a\right)\left(1-cos^2a\right)\)
\(=\left(1+\dfrac{sin^2a}{cos^2a}\right).cos^2a-\left(1+\dfrac{cos^2a}{sin^2a}\right).sin^2a\)
\(=cos^2a+sin^2a-sin^2a-cos^2a=\)\(0\)
Vậy B=0


Chọn C.
Ta có A = sin 2a.tan2a + 4sin2a - tan2a + 3cos2a
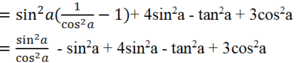
= 3sin2a + 3cos2a = 3.


\(\tan^2\alpha-\sin^2\alpha\cdot\tan^2\alpha\)
\(=\tan^2\alpha\cdot\left(1-\cos^2\alpha\right)\)
\(=\tan^2\alpha\cdot\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)\)
\(\tan^2\alpha-\sin^2\alpha\cdot\tan^2\alpha\\ =\tan^2\alpha\left(1-\sin^2\alpha\right)=\tan^2\alpha\cdot\cos^2\alpha\\ =\dfrac{\sin^2\alpha}{\cos^2\alpha}\cdot\cos^2\alpha=\sin^2\alpha\\ =1-\cos^2\alpha=\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)\)
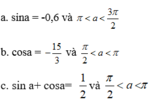
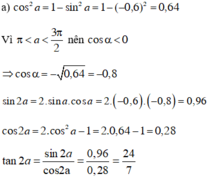
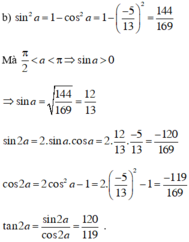
\(A=\dfrac{tan^2a-sin^2a}{cot^2a-cos^2a}\)
\(A=\dfrac{\dfrac{sin^2a}{cos^2a}-sin^2a}{\dfrac{cos^2a}{sin^2a}-cos^2a}=\dfrac{sin^2a\left(\dfrac{1}{cos^2a}-1\right)}{cos^2a\left(\dfrac{1}{sin^2a}-1\right)}\)
\(A=\dfrac{sin^2a\left(\dfrac{1-cos^2a}{cos^2a}\right)}{cos^2a\left(\dfrac{1-sin^2a}{sin^2a}\right)}=\dfrac{sin^2a\left(\dfrac{sin^2a}{cos^2a}\right)}{cos^2a\left(\dfrac{cos^2a}{sin^2a}\right)}\)
\(A=\dfrac{\dfrac{sin^4a}{cos^2a}}{\dfrac{cos^4a}{sin^2a}}=\dfrac{sin^4a}{cos^2a}.\dfrac{sin^2a}{cos^4a}\)
\(A=\dfrac{sin^6a}{cos^6a}=tan^6a\)