Cho \(m< n\), chứng tỏ :
a) \(2m+1< 2n+1\)
b) \(4\left(m-2\right)< 4\left(n-2\right)\)
c) \(3-6m>3-6n\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
4 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
NQ
2
4 tháng 5 2017
a. Ta có: m<n
<=> 2m<2n (nhân cả hai vế với 2)
<=> 2m+1<2n+1 (cộng cả hai vế với 1) \(\xrightarrow[]{}\) đpcm
b. Ta có: m<n
<=> m-2<n-2 (cộng cả hai vế với -2)
<=> 4(m-2)<4(n-2) (nhân cả hai vế với 4) \(\xrightarrow[]{}\) đpcm
4 tháng 5 2017
c. Ta có: m<n
<=> -6m>-6n (nhân cả hai vế với -6)
<=> 3-6m>3-6n (cộng cả hai vế với 3) \(\xrightarrow[]{}\) đpcm
d. Ta có: m<n
<=> 4m<4n (nhân cả hai vế với 4)
<=> 4m+1<4n+1 (cộng cả hai vế với 1)
mà 4n+1<4n+5
=> 4m+1<4n+5 \(\xrightarrow[]{}đpcm\)
P
18 tháng 3 2018
a, vì m>n
=> m+7>n+7
b, vì m>n
=> -2m<-2n
=>-2m-8<-2n-8
c, vì m>n
=>m+1>n+1
mà m+3>m+1
=>m+3>n+1
phần d,e,f máy mình cùi nên không hiện ra phép tính. sr nhiều
SE
18 tháng 3 2018
m>n
a) m+7 và m+7
ta có : m>n
=> m+7 > n+7
b) -2m+8 và -2n+8
ta có : m>n
=> -2m > -2n
=> -2m+8 > -2n+8
c) m+3 và m+1
ta có : 3 >1
=> m+3 > m+1
d) \(\dfrac{1}{2}\) \(\left(m-\dfrac{1}{4}\right)\)và\(\dfrac{1}{2}\)\(\left(n-\dfrac{1}{4}\right)\)
ta có: m > n
=> \(m-\dfrac{1}{4}\) > \(n-\dfrac{1}{4}\)
=>\(\dfrac{1}{2}\left(m-\dfrac{1}{4}\right)\)>\(\dfrac{1}{2}\left(n-\dfrac{1}{4}\right)\)
e) \(\dfrac{4}{5}-6\)m và \(\dfrac{4}{5}-6n\)
ta có : m > n
=> -6m > -6n
=> \(\dfrac{4}{5}-6m>\dfrac{4}{5}-6n\)
f) \(-3\left(m+4\right)+\dfrac{1}{2}\) và \(-3\left(n+4\right)+\dfrac{1}{2}\)
ta có : m > n
=> m=4 > n+4
=> -3(m+4) > -3(m+4)
=>\(-3\left(m+4\right)+\dfrac{1}{2}>-3\left(n+4\right)+\dfrac{1}{2}\)
22 tháng 2 2022
a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: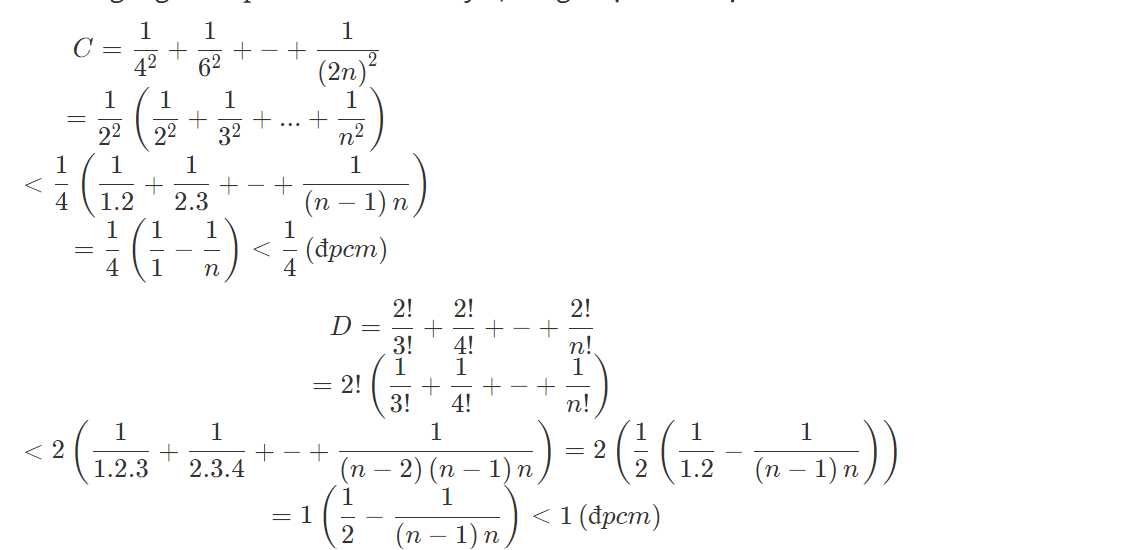 
BK
4 tháng 5 2017
bài 1:
a) 4n+4+3n-6<19
<=> 7n-2<19
<=> 7n<21 <=> n< 3
b) n\(^2\) - 6n + 9 - n\(^2\) + 16\(\leq\)43
-6n+25\(\leq\)43
-6n\(\leq\)18
n\(\geq\)-3
23 tháng 5 2022
a: \(\left(n^2+3n-1\right)\left(n+2\right)-n^3+2\)
\(=n^3+2n^2+3n^2+6n-n-2+n^3+2\)
\(=5n^2+5n=5\left(n^2+n\right)⋮5\)
b: \(\left(6n+1\right)\left(n+5\right)-\left(3n+5\right)\left(2n-1\right)\)
\(=6n^2+30n+n+5-6n^2+3n-10n+5\)
\(=24n+10⋮2\)
d: \(=\left(n+1\right)\left(n^2+2n\right)\)
\(=n\left(n+1\right)\left(n+2\right)⋮6\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 2 2020
a/ \(=lim\frac{\left(-\frac{2}{3}\right)^n+1}{-2.\left(-\frac{2}{3}\right)^n+3}=\frac{1}{3}\)
b/ \(=lim\frac{\left(2-\frac{1}{n}\right)\left(1+\frac{1}{n}\right)\left(3+\frac{4}{n}\right)}{\left(\frac{5}{n}-6\right)^3}=\frac{2.1.3}{\left(-6\right)^3}=-\frac{1}{36}\)
c/ \(=lim\frac{5n+3}{\sqrt{n^2+5n+1}+\sqrt{n^2-2}}=\frac{5+\frac{3}{n}}{\sqrt{1+\frac{5}{n}+\frac{1}{n^2}}+\sqrt{1-\frac{2}{n}}}=\frac{5}{1+1}=\frac{5}{2}\)
d/ \(=lim\frac{5.\left(\frac{1}{2}\right)^n-6}{4.\left(\frac{1}{3}\right)^n+1}=\frac{-6}{1}=-6\)
e/ \(=-n^3\left(2+\frac{3}{n}-\frac{5}{n^2}+\frac{2020}{n^3}\right)=-\infty.2=-\infty\)
AH
Akai Haruma
Giáo viên
23 tháng 5 2021
Lời giải:
\(M=\frac{1.2.3.4.5.6.7...(2n-1)}{2.4.6...(2n-2).(n+1)(n+2)....2n}=\frac{(2n-1)!}{2.1.2.2.2.3...2(n-1).(n+1).(n+2)...2n}\)
\(=\frac{(2n-1)!}{2^{n-1}.1.2...(n-1).(n+1).(n+2)....2n}=\frac{(2n-1)!}{2^{n-1}.1.2...(n-1).n(n+1)..(2n-1).2}\)
\(=\frac{(2n-1)!}{2^{n-1}.(2n-1)!.2}=\frac{1}{2^{n-1}.2}<\frac{1}{2^{n-1}}\)
Ta có đpcm.
