cho tam giác ABC, gọi D là trung điểm AB trên cạnh AC lấy E sao cho AE=2EC. gọi O là giao điểm của CD và BE. cmr: BO=3EO
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hình bạn tự vẽ nha
Xét tam giác ABE và tam giác ACD có
AB=AC ( gt)
AD=AE ( gt)
góc BAC chung
=> tam giác ABE= tam giác ACD
=> BE=CD (đpcm)

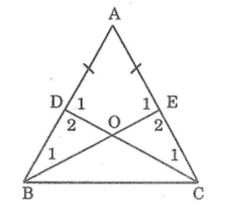
ΔBEA= ΔCDA (chứng minh trên)
⇒∠(B1 ) =∠(C1 ) ;∠(E1 ) =∠(D1 ) (hai góc tương ứng) (1)
+) Ta có: ∠(E1 ) +∠(E2 ) =180o (hai góc kề bù) (2)
Và ∠(D1 ) +∠(D2 ) =180o (hai góc kề bù) (3)
Từ (1); (2) và (3) suy ra: ∠(E2 ) =∠(D2 )
+) Theo giả thiết ta có; AB = AC
Và AD = AE
Lấy vế trừ vế, suy ra:
AB - AD = AC - AE hay BD = CE
Xét ΔOEC và ΔOCE, ta có:
∠(D2 ) =∠(E2 ) (chứng minh trên)
DB=EC (chứng minh trên)
∠(B1 ) =∠(C1 ) (chứng minh trên)
Suy ra: ΔODB= ΔOCE ( g.c.g)

a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
b: Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Xét ΔBOD và ΔCOE có
\(\widehat{ODB}=\widehat{OEC}\)
DB=EC
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔBOD=ΔCOE

a: Xét ΔABE và ΔACD có
AB=AC
\(\stackrel\frown{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD

Từ E dựng đường thẳng //AB cắt CD tại I và BC tại K
=> \(\frac{CE}{CA}=\frac{CK}{CB}=\frac{1}{3}\) (Talet trong tg) (1)
Xet tam giác ADC có \(\frac{CE}{CA}=\frac{IE}{DA}\) (Talet trong tg) (2)
Xét tg BDC có \(\frac{CK}{CB}=\frac{IK}{DB}\) (Talet trong tg) (3)
Từ (1) (2) và (3) \(\Rightarrow\frac{IE}{DA}=\frac{IK}{DB}=\frac{1}{3}\) Mà \(DA=DB\Rightarrow IE=IK\Rightarrow\frac{IE}{DB}=\frac{1}{3}\)
Xét tg OIE và tg ODB có
\(\widehat{OEI}=\widehat{OBD}\) (góc so le trong)
\(\widehat{EOI}=\widehat{BOD}\) (góc đối đỉnh)
=> tg OIE đồng dạng với tg ODB (g.g.g)\(\Rightarrow\frac{EO}{BO}=\frac{IE}{DB}=\frac{1}{3}\Rightarrow BO=3EO\)