Trong không gian Oxyz hãy xác định tâm và bán kính các mặt cầu có phương trình sau đây :
a) \(x^2+y^2+z^2-6x+2y-16z-26=0\)
b) \(2x^2+2y^2+2z^2+8x-4y-12z-100=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 7 2017
Đáp án B.
x 2 + y 2 + z 2 − 2 x + 4 y − 6 z − 2 = 0 ⇔ x − 1 2 + y + 2 2 + z − 3 2 = 1 + 4 + 9 + 2 = 16 ⇒ I 1 ; − 2 ; 3 , R = 4.
CM
27 tháng 9 2018
Đáp án A
Ta có (S): (x+1)²+(y-2)²+(z+3)²=16.
Do đó mặt cầu (S) có tâm I(-1;2;-3) và bán kính R=4.
CM
25 tháng 9 2018
Chọn C
Mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 có tâm I (1; -2; 2) bán kính R = 5
Khoảng cách từ I (1; -2; 2) đến mặt phẳng (P): x + 2y - 2z - 2 = 0 là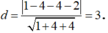 
Mặt phẳng cắt mặt cầu theo giao tuyến là một đường tròn có bán kính là: 
a) Tâm \(I\left(3;-1;8\right)\), bán kính \(r=10\)
b) Tâm \(I\left(-2;1;3\right)\), bán kính \(r=8\)