Cho hàm số \(y=\dfrac{1}{4}x^3-\dfrac{3}{2}x^2+5\)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho
b) Tìm các giá trị của tham số m để phương trình \(x^3-6x^2+m=0\) có 3 nghiệm phân biệt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
23 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
13 tháng 1 2018
a) Tập xác định: D = R;
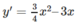
y′= 0 ⇔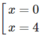 
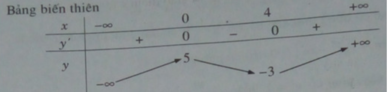
Hàm số đồng biến trên mỗi khoảng (– ∞ ; 0), (4; + ∞ ).
Hàm số nghịch biến trên mỗi khoảng (0; 4).
Hàm số đạt cực đại tại x = 0, y C Đ = 5. Hàm số đạt cực tiểu tại x = 4, y C T = -3.
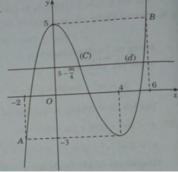
Đồ thị đi qua A(-2; -3); B(6;5).
b) x 3 – 6 x 2 + m = 0
⇔ x 3 – 6 x 2 = –m (1)
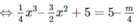
Số nghiệm thực phân biệt của phương trình (1) bằng số giao điểm phân biệt của đồ thị (C)
và đường thẳng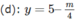 
Suy ra (1) có 3 nghiệm thực phân biệt khi và chỉ khi:
CM
22 tháng 2 2018
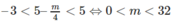
a) TXĐ: D = R
Sự biến thiên:
y′ = 3 x 2 – 6x = 3x(x – 2)
y′=0 ⇔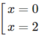 
Hàm số đồng biến trên mỗi khoảng (– ∞ ;0), (2;+ ∞ )
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0 ; y C Đ = y(0) = 0
Hàm số đạt cực tiểu tại x = 2; y C T = y(2) = -4.
Giới hạn: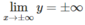 
Điểm uốn: y” = 6x – 6, y” = 0 ⇔ x = 1; y(1) = –2
Suy ra đồ thị có điểm uốn I(1; -2)
Bảng biến thiên:
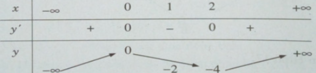
Đồ thị:
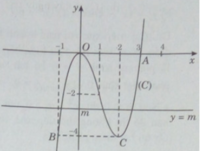
Đồ thị cắt trục hoành tại O(0;0), A(3;0). Đồ thị đi qua điểm B(-1;-4); C(2;-4).
b) x 3 – 3 x 2 – m = 0 ⇔ x 3 – 3 x 2 = m x 3 – 3 x 2 – m = 0 ⇔ x 3 – 3 x 2 = m (∗)
Phương trình (∗) có 3 nghiệm phân biệt khi và chỉ khi đường thẳng y = m cắt (C) tại 3 điểm phân biệt. Từ đó suy ra: – 4 < m < 0.
14 tháng 4 2017
Lời giải
khảo sát
TXD mọi x
y' =3x^2 -6x =3x(x-2)
y' =0 => x= 0 hoặc x=2
y'' =6x-6
y''(0) =-6 <0 hàm đạt cực đại tại x=0
y''(2) =6 >0 hàm đạt cực tiểu tại x =2
y'' =0 => x=1 hàm có điểm uốn tại x=1
hàm đi từ - vc--> +vc đi góc (III) lên (IV)
Vẽ đồ thị
Các điểm quan trọng
cực đại A(0,0)
cực tiểu B(2,-4)
uốn C(1,-2)
Các điểm phụ trọng
giao với trục hoành E(0,0); \(F\left(3;0\right)\)
Giao với trục tung: \(A\left(0,0\right)\)
Đồ thị
b)
nhìn vào đồ thị số y=x^3 -3x^2
Hàm số x^3 -3x^2 -m có 3 nghiệm phân biệt
khi 0<m<-4
CM
13 tháng 8 2018
a) Tập xác định: D = R
y′=0 ⇔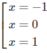 
Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; + ∞ )
Hàm số nghịch biến trên mỗi khoảng (− ∞ ; −1); (0; 1)
Hàm số đạt cực đại tại x = 0; y C Đ = 0
Hàm số đạt cực tiểu tại x = 1 hoặc x = -1; y C T = −2
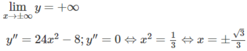
Đồ thị có hai điểm uốn:
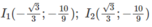
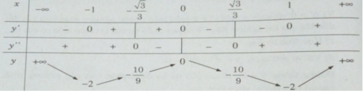
Bảng biến thiên:
Đồ thị:
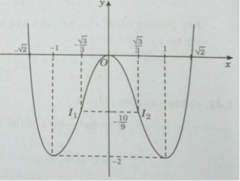
Đồ thị cắt trục hoành tại:
b) Ta có: x 2 | x 2 − 2| = m
⇔ 2 x 2 | x 2 − 2| = 2m
⇔|2 x 2 ( x 2 − 2)| = 2m
⇔|2 x 4 − 4 x 2 | = 2m
Từ đồ thị hàm số y = 2 x 4 – 4 x 2 có thể suy ra đồ thị của hàm số y = |2 x 4 − 4 x 2 | như sau:
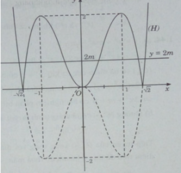
Phương trình: |2 x 4 − 4 x 2 | = 2m có 6 nghiệm phân biệt khi và chỉ khi đường thẳng y = 2m có 6 nghiệm phân biệt với đồ thị (H)
⇔ 0 < 2m < 2
⇔ 0 < m < 1
H
31 tháng 3 2017
a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
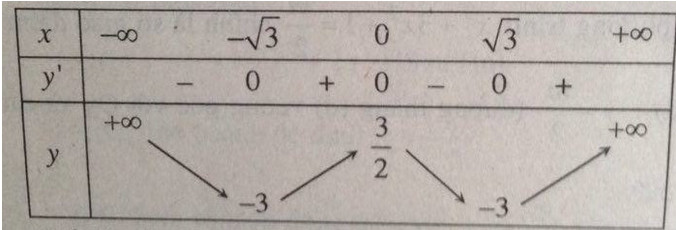
Bảng biến thiên:
Đồ thị hàm số:
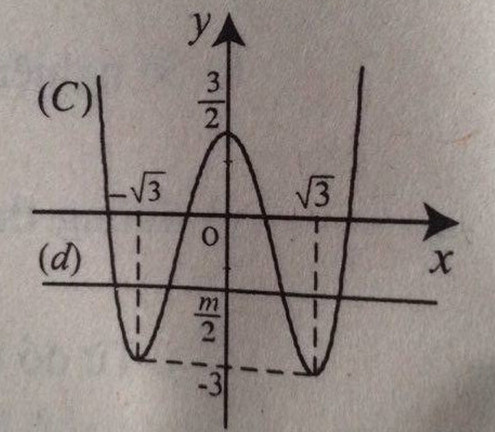
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm
