Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
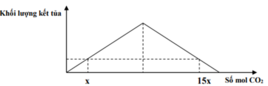
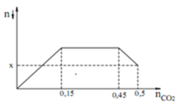
Nhận thấy đồ thị biểu diễn kết tủa phụ thuộc vào CO2 là tam giác vuông cân
Vậy tại điểm cực đại số mol của CO2 là trung điểm của x và 15x
⇒ Tại điểm cực đại số mol của CO2 là x + 15 x - x 2 = 8x
⇒ nCa(OH)2 = nCO2 = 0,2 → 8x= 0,2 ⇒ x = 0,025

Đáp án D
Nhận thấy đồ thị có các giai đoạn:
+Giai đoạn kết tủa tăng dần do Ca(OH)2 tác dụng với CO2 tạo kết tủa CaCO3.
+Giai đoạn kết tủa không đổi do CO2 tác dụng với KOH.
+Giai đoạn kết tủa giảm dần do CO2 tác dụng với CaCO3 và hòa tan kết tủa này (tạo Ca(HCO3)2).
![]()
Lúc CO2 đạt 0,5 mol thì kết tủa đã bị hòa tan mất 0,05 mol (do từ 0,45 mol đã bắt đầu hòa tan kết tủa).
=> x = 0,15 - 0,05 = 0,1 mol

Giải thích:
nH2 = nBa = nBaO = nBa(OH)2 => Ba(OH)2 sau pư = 3a mol
Tại nCO2 = 3,6a mol:
BaCO3: 0,192 mol
Ba(HCO3)2: 3a-0,192
BTNT C: 0,192+2(3a-0,192) = 3,6a => a = 0,08 mol
m = 0,08.137+0,08.153+0,08.171 = 36,88 gam
Đáp án C

Giải thích:
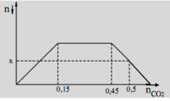
Quan sát đồ thị ta thấy nCO2 = 0,15 thì kết tủa đạt max.
=> nCa(OH)2 = nCaCO3 max = 0,15
Khi nCO2 = 0,45 thì bắt đầu hòa tan kết tủa.
Khi nCO2 = 0,5 thì lượng kết tủa bị hòa tan là: nCaCO3 bị hòa tan = 0,5 - 0,45 = 0,05
=> nCaCO3 còn lại = x = 0,15 - 0,05 = 0,1
Đáp án A

Đáp án A
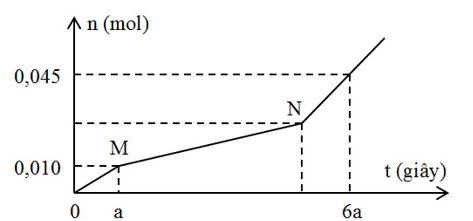
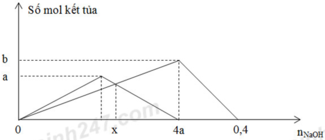
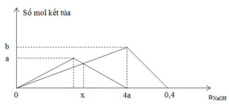
*Tại nOH- = 0,4 mol (thí nghiệm 2): Al(OH)3 vừa bị hòa tan hết
=> nOH- = 4nAl3+ => 0,4 = 4b => b = 0,1 mol
*Tại nOH- = 4a (thí nghiệm 2): Al(OH)3 đạt cực đại
=> nOH- = 3nAl(OH)3 => 4a = 3b => a = 3b/4 = 0,075 mol
*Tại nOH- = x mol: Giả sử nAl(OH)3 = nZn(OH)2 = y mol
- Thí nghiệm 2: Al(OH)3 chưa đến cực đại
nOH- = 3nAl(OH)3 => x = 3y (1)
- Thí nghiệm 1: Zn(OH)2 bị tan một phần
nOH- = 4nZn2+ - 2nZn(OH)2 => x = 4.0,075 – 2.y (2)
Giải (1) và (2) => x = 0,18; y = 0,06
=> m = mZn(OH)2 + mAl(OH)3 = 0,06.99 + 0,06.78 = 10,62 gam ≈ 10,6 gam

Đáp án A
*Tại nOH- = 0,4 mol (thí nghiệm 2): Al(OH)3 vừa bị hòa tan hết
=> nOH- = 4nAl3+ => 0,4 = 4b
=> b = 0,1 mol
*Tại nOH- = 4a (thí nghiệm 2): Al(OH)3 đạt cực đại
=> nOH- = 3nAl(OH)3 => 4a = 3b
=> a = 3b/4 = 0,075 mol
*Tại nOH- = x mol: Giả sử nAl(OH)3 = nZn(OH)2 = y mol
- Thí nghiệm 2: Al(OH)3 chưa đến cực đại
nOH- = 3nAl(OH)3 => x = 3y (1)
- Thí nghiệm 1: Zn(OH)2 bị tan một phần
nOH- = 4nZn2+ - 2nZn(OH)2
=> x = 4.0,075 – 2.y (2)
Giải (1) và (2) => x = 0,18; y = 0,06
=> m = mZn(OH)2 + mAl(OH)3 = 0,06.99 + 0,06.78 = 10,62 gam ≈ 10,6 gam
Áp dụng CT nhanh: nHNO3 = 12nN2 + 10nNH4+ = 12.0,03+ 10.0,09 = 1,26 (mol)
=> VHNO3 = 1,26.22,4 = 5,04 (lít)






a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
Đồ thị hàm số:
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm