Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyens SA và cát tuyens SBC của đường tròn. Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


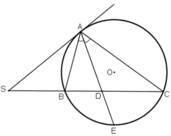
Tia phân giác AD cắt (O) tại E.
+  là góc có đỉnh nằm bên trong đường tròn
là góc có đỉnh nằm bên trong đường tròn
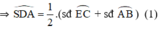
+ 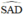 là góc tạo bởi tiếp tuyến AS và dây AE
là góc tạo bởi tiếp tuyến AS và dây AE
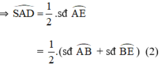
+ 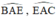 lần lượt là các góc nội tiếp chắn các cung
lần lượt là các góc nội tiếp chắn các cung 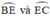
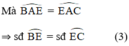
Từ (1); (2) và (3) suy ra 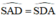
⇒ ΔSAD cân tại S
⇒ SA = SD.

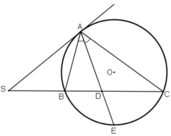
Tia phân giác AD cắt (O) tại E.
+  là góc có đỉnh nằm bên trong đường tròn
là góc có đỉnh nằm bên trong đường tròn
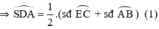
+ 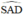 là góc tạo bởi tiếp tuyến AS và dây AE
là góc tạo bởi tiếp tuyến AS và dây AE
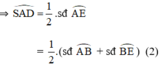
+ 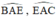 lần lượt là các góc nội tiếp chắn các cung
lần lượt là các góc nội tiếp chắn các cung 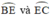
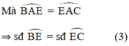
Từ (1); (2) và (3) suy ra 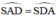
⇒ ΔSAD cân tại S
⇒ SA = SD.
Kiến thức áp dụng
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn.
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

Gọi giao của AD và (O) là E
\(\widehat{ADS}=\dfrac{sđ\stackrel\frown{AB}+sđ\stackrel\frown{CE}}{2}=\dfrac{sđ\stackrel\frown{AB}+sđ\stackrel\frown{BE}}{2}\)(Vì cung BE=cung CE)
\(\widehat{SAD}=\dfrac{sđ\stackrel\frown{AB}+sđ\stackrel\frown{BE}}{2}\)
Do đó: góc SDA=góc SAD
=>ΔSDA cân tại S
=>SA=SD

a.
Ta có \(\widehat{SAD}=\widehat{ACE}\) (góc nội tiếp và góc tiếp tuyến cùng chắn cung AE)
Lại có \(\widehat{ADB}\) là góc có đỉnh nằm trong đường tròn
\(\Rightarrow\widehat{ADB}=\dfrac{1}{2}\left(sđ\stackrel\frown{AB}+sđ\stackrel\frown{CE}\right)=\widehat{ACB}+\widehat{CAE}\)
Mà \(\widehat{ACB}=\widehat{SAB}\) (cùng chắn cung AB) và \(\widehat{CAE}=\widehat{BAE}\) (do AE là phân giác \(\widehat{BAC}\))
\(\Rightarrow\widehat{ADB}=\widehat{SAB}+\widehat{BAE}=\widehat{SAD}\Rightarrow\Delta SAD\) cân tại S
\(\Rightarrow SA=SD\)
b.
Xét hai tam giác SAB và SCA có:
\(\left\{{}\begin{matrix}\widehat{ASB}\text{ chung}\\\widehat{SAB}=\widehat{ACB}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta SAB\sim\Delta SCA\left(g.g\right)\)
\(\Rightarrow\dfrac{SA}{SC}=\dfrac{SB}{SA}\Rightarrow SA^2=SB.SC\)
Theo câu a ta có \(SA=SD\)
\(\Rightarrow SD^2=SB.SC\)

keo dai AD cắt (O) tại E
- DAD=DAC=>cung BE=cungEC
- SDA=1/2 sđcung AB+1/2 sđ cung EC
- SAE=1/2 sđ AE=1/2sđ AB+1/2 sđ BE
=> góc SAE= góc SDA
=> tam giác SAD cân tai S
=>SA=SD

a: góc SAM=góc SAB+góc BAM
góc SMA=góc SCA+góc MAC
mà góc SAB=góc SCA và góc BAM=góc CAM
nên góc SAM=góc SMA
=>SM=SA
b: góc SGO=90 độ
Vì góc SAO=góc SGO
=>SAGO nọpi tiếp
=>góc SGA=góc SOA=1/2*góc DOA=1/2*sđ cung AD
=>góc SAD=góc SGA
=>ΔSAF đồng djng với ΔSGA
=>SA/SG=SF/SA
=>SA^2=SG*SF
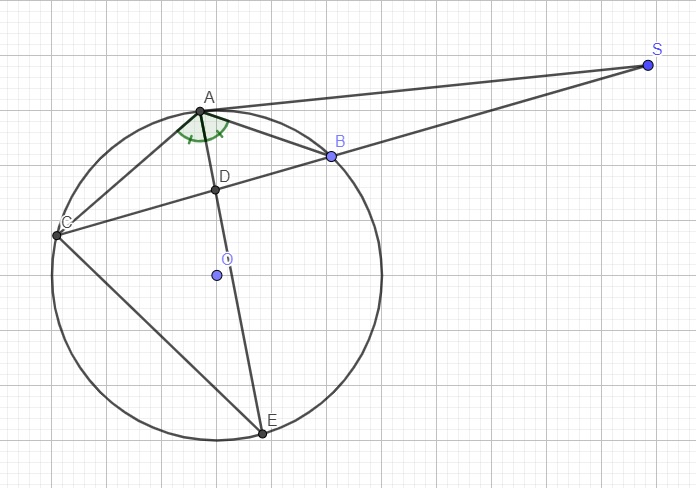
Lấy hình của Bastkoo.
Lời giải: