Tam giác ABC có \(\widehat{A}=120^0\). Tính cạnh BC cho biết cạnh AC =m và AB = n ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

18 tháng 6 2023
\(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\)
=>BC/sin120=a/sin30=2a
=>BC=a*căn 3
PT
1

CM
3 tháng 4 2017
Áp dụng định lý côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A
= m2 + n2 – 2.m.n.cos120º
= m2 + n2 + mn.
⇒ BC = √( m2 + n2 + mn).

12 tháng 4 2017
Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{A}=75^o\)
* \(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\Rightarrow AB=\dfrac{BCsinC}{sinA}=a\left(1+\sqrt{3}\right)\)
* \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}\Rightarrow AC=\dfrac{BCsinB}{sinA}=a\left(\dfrac{-6+3\sqrt{2}}{2}\right)\)
Ta có: BC2 = AC2 + AB2 - 2AB.AC. cos1200
=> BC2 = m2 + n2 - 2m.n (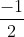 )
)
=> BC2 = m2 + n2 + m.n
=> BC =