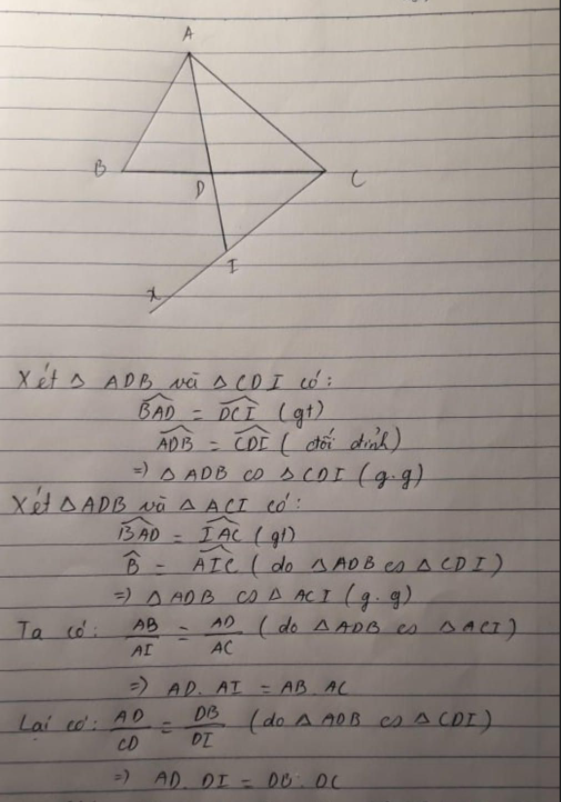cho tam giác ABC, phân giác AD. Trên nửa mặt phẳng bờ BC ko chứa điểm A vẽ tia Bx tạo với BC 1 góc bằng góc ABD. Gọi I là giao điểm của Bx và AD kéo dài. a) Tg ADC và BDI có đồng dạng ko? Vì sao? b) Cm: AB.AC=AD.AI c) Cm: AB.AC-DB.BC=AD bình phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
30 tháng 3 2021
Bài giải
a,
\(\widehat{DAC}=\widehat{BAD}=\widehat{DBI}\)( AD là tia phân giác \(\widehat{BAC}\) )
\(\widehat{ADC}=\widehat{BDI}\)
\(\Rightarrow\Delta ADC\sim\Delta BDI\left(g.g\right)\)
b, \(\Delta ADC\sim\Delta BDI\left(cmt\right)\Rightarrow\widehat{AIB}=\widehat{ACD}\)
\(\widehat{BAD}=\widehat{DAC}\)
\(\Rightarrow\Delta ABI\sim\Delta ADC\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AI}=\dfrac{AD}{AC}\Rightarrow AB.AC=AD.AI\)
27 tháng 6 2023
a: Xét ΔDAB và ΔDCI có
góc DAB=góc DCI
góc ADB=góc CDI
=>ΔDAB đồng dạng với ΔDCI
=>DA/DC=DB/DI
=>DA/DB=DC/DI
Xét ΔDAC và ΔDBI có
DA/DB=DC/DI
góc ADC=góc BDI
=>ΔDAC đồng dạng với ΔDBI
b: Xét ΔABD và ΔAIC có
góc ABD=góc AIC
góc bAD=góc IAC
=>ΔABD đồng dạng với ΔAIC
=>AB/AI=AD/AC
=>AB*AC=AD*AI
26 tháng 1 2022
a) Xét tam giác MBD và tam giác MAB:
\(\widehat{DMB}chung.\)
\(\widehat{DBM}=\widehat{BAM}\left(\widehat{CBx}=\widehat{BAD}\right).\)
=> Tam giác MBD \(\sim\) Tam giác MAB (g - g).
