Cho S.ABCD, ABCD là hình vuông cạnh A, tam giác SAB đều, (SAB) vuông góc với đáy. M,N,P lần lượt là trung điểm BC, SD,SB. Tính d (AP, MN).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 11 2017
Chọn B.
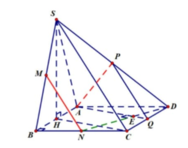
Gọi Q là trung điểm CD, ta có PQ//SC//MN nên MN//(APQ)
=> d(MN, PQ)=d(MN, (APQ))=d(N,(APQ))
Vì N D ⊥ H C N D ⊥ S H ⇒ N D ⊥ ( S H C )
⇒ N D ⊥ S C ⇒ N D ⊥ P Q
A Q → . N D → = ( A D → + D Q → ) . ( D C → + C N → ) = 0 → ⇒ A Q ⊥ N D
Vậy có
N D ⊥ P Q N D ⊥ A Q ⇒ N D ⊥ A P Q t ạ i E ⇒ d ( M N , A P ) = N E
Mà có
1 D E 2 = 1 D A 2 + 1 D Q 2 = 5 a 2 ⇒ D E = a 5
Và D N = a 5 2 ⇒ E N = 3 a 5 10
Vậy d ( M N , A P ) = 2 a 10
CM
30 tháng 9 2019
Đáp án C.
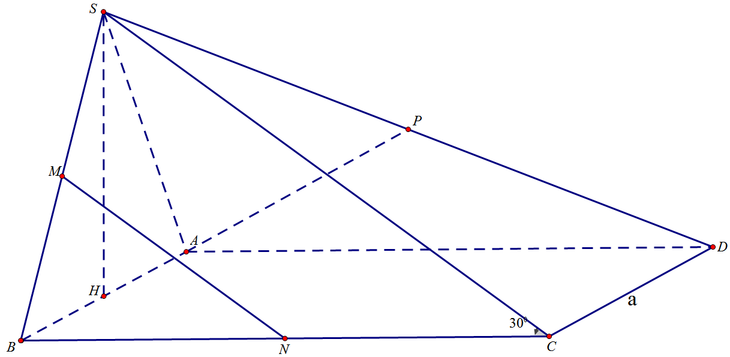
Trong không gian Oxyz:
Chọn A ≡ O 0 ; 0 ; 0 ; B a ; 0 ; 0 ; D 0 ; a ; 0 ; C a ; a ; 0
⇒ H a 2 ; 0 ; 0 ; S a 2 ; 0 ; a 3 2 ; M 3 a 4 ; 0 ; a 3 4 ; N a ; a 2 ; 0 ; P a 4 ; a 2 ; a 3 4
Ta có:
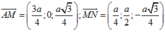
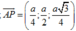
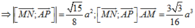
⇒ d M N ; A P = M N → ; A P → . A M → M N → ; A P → = 3 5 10 a
Gọi H là trung điểm AB thì \(SH\perp\left(ABCD\right)\)
Gọi E là trung điểm DH thì NE là đường trung bình trong tam giác SHD nên \(NE||SH\)
Đồng thời ME là đường trung bình trong hình thang BCDH nên \(ME||AB\)
\(\Rightarrow\left(MNE\right)||\left(SAB\right)\)
\(\Rightarrow d\left(AP,MN\right)=d\left(\left(MNE\right);\left(SAB\right)\right)=BM=\dfrac{a}{2}\)