Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
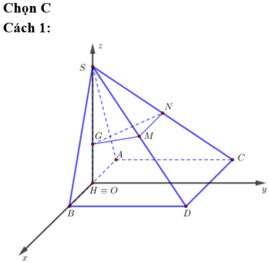
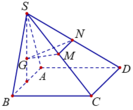
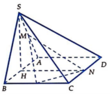
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó
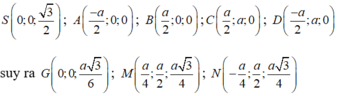
Ta có mặt phẳng (ABCD) có vectơ pháp tuyến là 
, mặt phẳng (GMN) có vectơ pháp tuyến là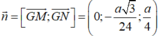 
Gọi (α) là góc giữa hai mặt phẳng (GMN) và (ABCD), ta có
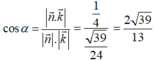
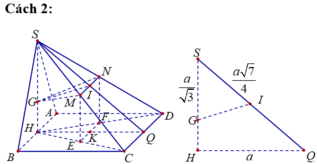
Gọi E, F lần lượt là hình chiếu của M và N lên (ABCD). Suy ra E, F lần lượt là trung điểm của HC, HD.
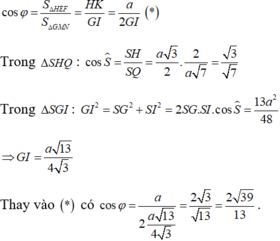
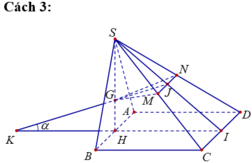
Gọi H, I lần lượt là trung điểm của AB, CD.
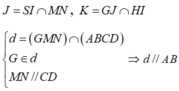
Mà d ⊥ (SIH) nên góc giữa góc giữa hai mặt phẳng (GMN) và (ABCD) là 
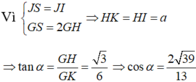
Chọn đáp án C
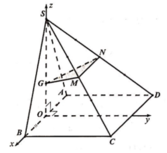
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên
Chọn hệ trục tọa độ Oxyz như hình vẽ. Chọn a = 2.
Khi đó: 
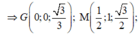
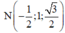
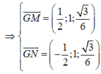
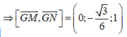
Ta có mặt phẳng (ABCD) có vecto pháp tuyến là 
Mặt phẳng (GMN) có vecto pháp tuyến là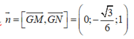 
Gọi α là góc giữa hai mặt phẳng (GMN) và (ABCD)
Ta có:
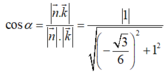
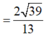
Gợi ý xem bạn làm được ko, ko thì để mình trình bày luôn
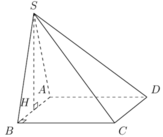
Kẻ \(KC\perp HD;KC\cap HD=\left\{K\right\}\)
\(\left\{{}\begin{matrix}KC\perp HD\\KC\perp SH\end{matrix}\right.\Rightarrow KC\perp\left(SHD\right)\Rightarrow\left(SKC\right)\perp\left(SHD\right)\)
Kẻ \(CI\perp SK;CI\cap SK=\left\{I\right\}\Rightarrow CI\perp\left(SHD\right)\Rightarrow CI\perp\left(SHD\right)\)
\(\Rightarrow\left(SC,\left(SHD\right)\right)=\left(SC,SI\right)\)
Đáp án là C
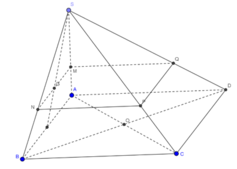
Cách 1. Ta có mặt phẳng (P) đi qua trọng tâm của tam giác SAB cắt các cạnh của khối chóp lần lượt tại M, N, P, Q. Với MN//AB, NP//BC, PQ//CD, QM//AD.
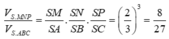
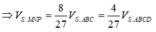
Tương tự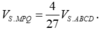 
Nên 
Đặt AB = x.
Ta có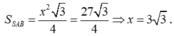 
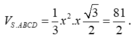
Từ đó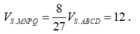 
Cách 2. Do hai khối chóp S.MNPQ, S.ABCD đồng dạng với nhau theo tỉ số k = 2 3 nên tỉ lệ thể tích là
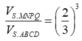
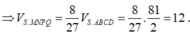
Đáp án B
Phương pháp:
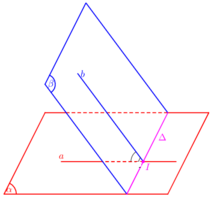
Xác định góc giữa hai mặt phẳng (α;β)
- Tìm giao tuyến Δ của (α;β)
- Xác định 1 mặt phẳng γ ⊥ Δ
- Tìm các giao tuyến a = α∩γ, b = β ∩ γ
- Góc giữa hai mặt phẳng (α;β):(α;β) = (a;b)
Cách giải:
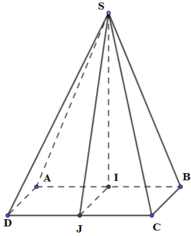
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB cân tại S ⇒ SI ⊥ AB
Vì mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD) nên SI ⊥ (ABCD)
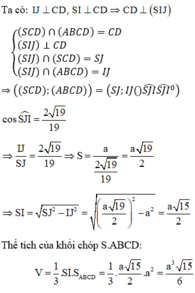
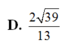
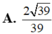
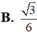
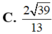
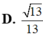
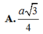
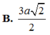
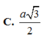
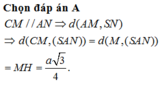
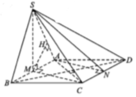
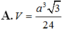
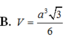
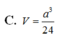
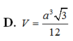
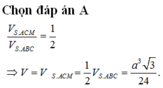
Đáp án D