Cho hình bình hành ABCD , đường chéo BD . Kẻ AH và CK vuông góc với BD tại H và K
. Chứng minh tứ giác AHCK là hình bình hành.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TC
Trên con đường thành công không có....
9 tháng 8 2021
Đúng(1)
Những câu hỏi liên quan
CM
9 tháng 12 2018
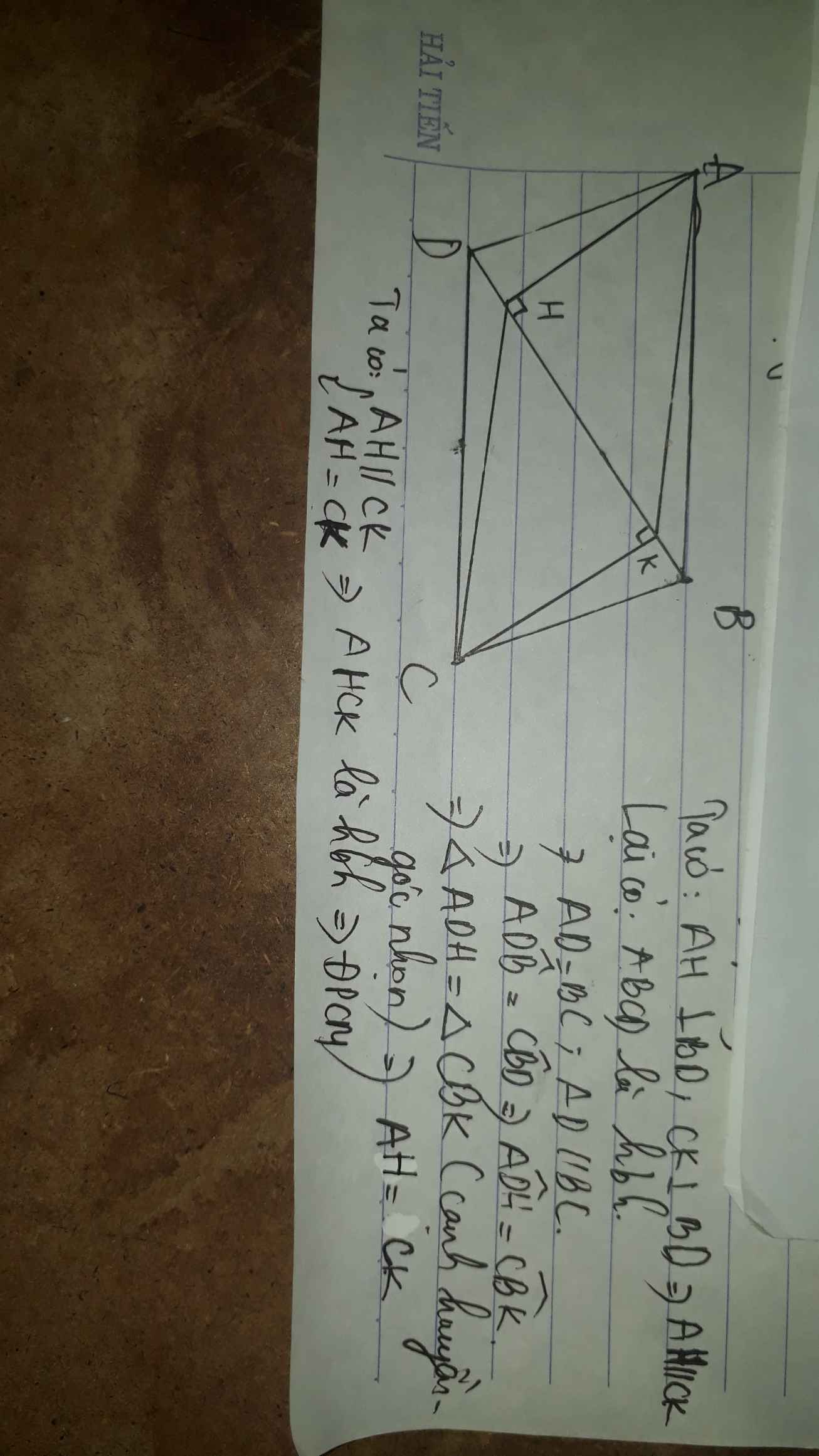
Ta chứng minh AH//CK, AH = CK (DAHD = DCKB) Þ AHCK là hình bình hành (cặp cạnh đối song song và bằng nhau)
NM
Nguyễn Minh Quang
Giáo viên
9 tháng 9 2021
ta có : hai tam giác ABD bằng CND ( do ABCD là hình bình hành nên )
\(S_{ABD}=S_{CBD}\Leftrightarrow\frac{1}{2}AH.BD=\frac{1}{2}CK.BD\Rightarrow AH=CK\)
mà AH song song với CK (do cùng vuông góc với BD)
nên AHCK là hình bình hành
G
9 tháng 9 2021
Giải thích các bước giải:
Ta có tứ giác ABCD là hình bình hành
=>AD// và =BC
AD//BC,cát tuyến BD
=>∠ADH=∠KBC(so le trong)
XétΔAHD và ΔBKC
·∠AHD=∠BKC=90 độ
·∠ADH=∠KBC
.AD=BC
=>ΔAHD = ΔBKC(ch+gn)
b)=>AH=CK(2 cạnh tương ứng của 2Δ=nhau) (1)
ta có AH⊥BD
CK⊥BC
=>AH//CK (2)
Từ (1) và (2) =>đpcm (theo tc đoạn chắn)
~ Chúc bn Thành Công trong HT ạ ~
27 tháng 9 2018
Xem ở đây nha:
Cho hình bình hành ABCD, Gọi H và K lần lượt là hình chiếu của A và C lên đường chéo BD. a) Chứng minh AHCK là hình bình hành. b) Gọi O là trung điểm của HK. Chứng minh ba điểm A, O, C thẳng hàng - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
27 tháng 9 2018
Xét tam giác vuông ADH & tam giác vuông CKB:
AD = BC ( ABCD là hbh)
góc D1= góc B1 ( so le trong)
=> tam giác vuông = tam giác vuông CKB ( cạnh hyền - góc nhọn)
=> AH = CK ( 2 cạnh t/ứng)
Xét tứ giác AHCK :
AH = CK (cmt)
AH // CK ( cùng vuông góc vs BD)
=> AHCK là hình bình hành ( đn)
