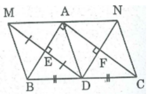
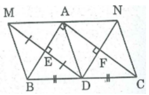
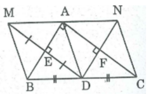
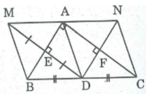
cho tam giác ABC vuông tại B, D là trung điểm của AC . E là điểm đối xứng với D qua AB , M là giao điểm của DE và AB . gọi F là điểm đối xứng với D qua BC, N là giao điểm của DF và BC
a) BMDN là hình gì? vì sao ?
b)BDCF là hình gì ? vì sao ?
c)tam giác ABC có thêm điều kiện gì thì tứ giác BMDN là hình vuông

a: Ta có: D và E đối xứng nhau qua AB
nên DE vuông góc với AB tại trung điểm của DE
=>M là trung điểm của DE
Ta có: D và F đối xứng nhau qua AC
nên DF vuông góc với AC tại trung điểm của DF
=>N là trung điểm của DF
Xét tứ giác BMDN có
\(\widehat{BMD}=\widehat{BND}=\widehat{NBM}=90^0\)
Do đó: BMDN là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của AC
DN//AB
Do đó: N là trung điểm của BC
Xét tứ giác BDCF có
N là trung điểm của BC
N là trung điểm của DF
Do đó:BDCF là hình bình hành
mà DB=DC
nên BDCF là hình thoi