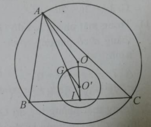
Bai1: Cho tam giác ABC nội tiếp đường tròn tâm O bán kính R. Các đỉnh B, C cố định còn A chạy trên đường tròn đó. Tìm tập hợp các trọng tâm G của tam giác ABC khi A di độngCho tam giác ABC nội tiếp đường tròn tâm O bán kính R. các bạn giúp mih` giải và vẽ hình bài này nhé help me đang cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 3 2017
Ta có tam giác OBC đều, đường cao OI = (R√3)/2
⇒ I chạy trên đường tròn tâm O bán kính (R√3)/2.
Vì A cố định, G là trọng tâm tam giác ABC nên A G → = 2 3 A I →
⇒ có phép vị tự tâm A tỉ số k = 2/3 biến đường tròn (O;(R√3)/2) thành đường tròn (O';R’) với R ' = R 3 2 . 2 3 = R 3 3
Chọn đáp án C
AH
Akai Haruma
Giáo viên
29 tháng 7 2021
Lời giải:
Gọi $M$ là trung điểm của $BC$. Do $BC$ cố định nên $M$ cố định.
Qua $G$ kẻ $GI\parallel AO$ với $I\in OM$
Theo Talet thì $\frac{GI}{AO}=\frac{MI}{MO}=\frac{GM}{MA}=\frac{1}{3}$
Mà $M,O$ cố định nên $I$ cố định.
$\frac{GI}{AO}=\frac{1}{3}\Rightarrow GI=\frac{AO}{3}=\frac{R}{3}$
Vậy trọng tâm $G$ luôn thuộc đường tròn $(I, \frac{R}{3})$ cố định.
CM
23 tháng 4 2017
B, C cố định nên trung điểm I của BC cũng cố định. G là trọng tâm tam giác ABC nên ta có I G → = 1 / 3 I A → ⇒ có phép vị tự I tỉ số k = 1/3 biến A thành G. A chạy trên (O) nên G chạy trên (O’) ảnh của O qua phép vị tự trên.
Đáp án C
