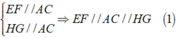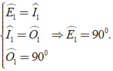Giúp mk với!!!
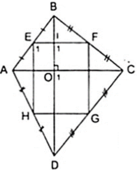
Cho tứ giác ABCD có 2 đường chéo AC và BD vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD và DA.
a) C/m: Bốn điểm E, F, G, H cùng thuộc một đường tròn.
b) Giả sử AB = 24 cm và BD = 18 cm. Tính bán kính của đường tròn đi qua bốn điểm E, F, G, H.