cho tam giác ABC đg cao AH gọi D , E ,M theo thứ tự là trung điểm của AB , AC, BC cma, DEMH là hinh thang cân b, gọi k là điểm đối xứng với h qua D tứ giác AKBH là hình gì ? vì saobài 2: cho tam giác nhon ABC có các đg cao BD và CF gọi H và K lần lượt là hình chiếu của B và C lên D,Ea, cm ; EH = EKb,nếu tam hiac ABC cân ở D thì tứ giác BCKH là hình gi ? vì...
Đọc tiếp
cho tam giác ABC đg cao AH gọi D , E ,M theo thứ tự là trung điểm của AB , AC, BC cm
a, DEMH là hinh thang cân
b, gọi k là điểm đối xứng với h qua D tứ giác AKBH là hình gì ? vì sao
bài 2: cho tam giác nhon ABC có các đg cao BD và CF gọi H và K lần lượt là hình chiếu của B và C lên D,E
a, cm ; EH = EK
b,nếu tam hiac ABC cân ở D thì tứ giác BCKH là hình gi ? vì sao?
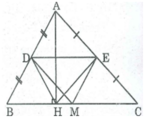
Bài 1:
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình
=>DE//BC
hay DE//HM
Xét ΔABC có
D là trung điểm của AB
M là trung điểm của BC
Do đó: DM là đường trung bình
=>DM=AC/2(1)
Ta có: ΔAHC vuông tại H
mà HE là đường trung tuyến
nên HE=AC/2(2)
Từ (1) và (2) suy ra DM=HE
Xét tứ giác DEMH có DE//HM
nên DEMH là hình thang
mà DM=HE
nên DEMH là hình thang cân
b: Xét tứ giác AKBH có
D là trung điểm của AB
D là trung điểm của HK
Do đó: AKBH là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AKBH là hình chữ nhật