cho tam giác ABC nhọn, 2 đường trung tuyến BM và CN cắt nhau tại I.Gọi E lvaf F là trung điểm của IB và IC
a) CM: Tứ giác MNEF là hình bình hành
b) CM: HE=NE/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 9 2016
a) Xét ΔABC ta có:
AN = NB
AM = MC
Suy ra MN là đường trung bình của Δ ABC
Nên MN song song với BC và MN=1/2 BC (1)
Xét Δ BIC ta có
IE = EB
IF = FC
Suy ra EF là đường trung bình của Δ BIC
Nên EF song song với BC và EF=1/2 BC(2)
Từ (1) và(2) suy ra EF =MN và EF song song với MN
Vậy MNEF là hình bình hành
QD
30 tháng 9 2016
Phần vẽ hình và ghi giả thuyết ,kết luận bạn tự làm nhé :)
a) Xét tam giác ABC ,ta có :
AN = NB (GT)
AM = MC (GT)
Nên MN là đường trung bình của tam giác ABC
=> MN // BC (1) , MN = 1/2 BC (2)
Xét tam giác BCI ,ta có :
BE = EI (GT)
CI = IF (GT)
Nên EF là đường trung bình của tam giác BIC
=> EF // BC (3) , EF = 1/2 BC (4)
Từ (1) và (3) => MN // EF (5)
Từ (2) và (4) => MN = EF (6)
Từ (5) và (6) => MNEF là hình bình hành ( Dấu hiệu nhận biết 3 )
b) Xét tứ giác EFHK ,ta có :
EF // HK (Vì H,K € BC ; mà BC// EF )
EH // FK (Vì H € NE ,K € MF ,mà NE // MF)
Do đó ,tứ giác EFKH là hình bình hành (Dấu hiệu nhận biết 1)
=> EF = HK (7)
mà EF = 1/2 BC [theo (4)] (8)
Từ (7) và (8) => HK = 1/2 BC
Câu c) tớ chưa nghĩ ra cách chứng minh
Cậu hãy tự suy nghĩ , chúc bạn may mắn
24 tháng 10 2021
Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
Do đó: NM là đường trung bình của ΔBAC
Suy ra: NM//BC và \(NM=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
E là trung điểm của GB
F là trung điểm của GC
Do đó: EF là đường trung bình của ΔGBC
Suy ra: EF//BC và \(EF=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra NM//FE và NM=FE
hay NMFE là hình bình hành
CM
22 tháng 7 2017
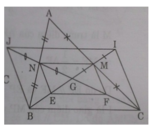
a) Ta có MN là đường trung bình của ΔABC
⇒ MN // BC và MN = BC/2
Tương tự EF là đường trung bình của ΔBGC nên EF // BC và EF = BC/2
Do đó MN // EF và MN = EF.
Vậy MNEF là hình bình hành (hai cạnh đối vừa song song vừa bằng nhau)
b) Ta có G là trong tâm của ΔABC nên GN = GC/2
Mà GN = JN (gt) ⇒ GJ = GC.
Tương tự ta có GI = GB
Vậy tứ giác BJIC là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
31 tháng 7 2021
a) Xét ΔABC có
N là trung điểm của AB(gt)
M là trung điểm của AC(gt)
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC và \(NM=\dfrac{BC}{2}\)(1)
Xét ΔGBC có
E là trung điểm của GB
F là trung điểm của GC
Do đó: EF là đường trung bình của ΔGBC
Suy ra: EF//BC và \(EF=\dfrac{BC}{2}\)(2)
Từ (1) và (2) suy ra NM//EF và NM=EF
hay MNEF là hình bình hành
b) Xét ΔABC có
BM là đường trung tuyến ứng với cạnh AC
CN là đường trung tuyến ứng với cạnh AB
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
Xét ΔABC có
G là trọng tâm của ΔABC
BM là đường trung tuyến ứng với cạnh AC
Do đó: \(GB=2GM\)
mà GF=2GM
nên GB=GF
hay G là trung điểm của BF
Xét ΔABC có
G là trọng tâm của ΔABC
CN là đường trung tuyến ứng với cạnh AB
Do đó: \(GC=2GN\)
mà GI=2GN
nên GC=GI
hay G là trung điểm của CI
Xét tứ giác BIFC có
G là trung điểm của đường chéo CI(cmt)
G là trung điểm của đường chéo BF(cmt)
Do đó: BIFC là hình bình hành
10 tháng 8 2019
a) Vì BM là trung tuyến AC
=> M là trung điểm AC (1)
Vì CN là trung tuyến AB
=> N là trung tuyến AB (2)
Từ (1) và (2) => MN là đường trung bình ∆ABC
=> MN //BC , MN = \(\frac{1}{2}BC\)
Vì E là trung điểm GB
F là trung điểm GC
=> FE là đường trung bình ∆GBC
=> FE//BC
=> FE = \(\frac{1}{2}BC\)
=> NM //FE
=> FE= NM
=> NMFE là hình bình hành
xét tam giác ABC ta có
M là trđ của AC( BM là đg trung tuyến)
N là trđ của AB (CN là đg trung tuyến)
suy ra MN là đg trung bình
suy ra MN//BC; MN= 1/2 BC
xét tam giác IBC ta có
E là trđ của IB(gt)
F là trđ của IC(gt)
suy ra EF là đg trung bình
suy ra EF//BC;EF=1/2BC
mà MN//BC;MN=1/2BC
nên EF//MN;EF=1/2BC
xét t/g MNEF ta có
EF//MN(cmt)
EF=MN(cmt)
suy ra t/g MNEF là hbh
Câu 2 tớ kg hiểu nói rõ hơn