tìm m để đồ thị hàm số \(y=mx^4-4x^2+1\) có 3 điểm cực trị là đỉnh của một tam giác vuông cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D
![]()
![]()
Hàm số có 3 điểm cực trị ⇔ m ≠ 0
Khi đó 3 điểm cực trị của đồ thị hàm số là
![]()
Do tính chất đối xứng, ta có ∆ A B C cân tại đỉnh A
Vậy ∆ A B C chỉ có thể vuông cân tại đỉnh A
![]()
Kết hợp điều kiện ta có: m = ± 1 ( thỏa mãn).
Lưu ý: có thể sử dụng công thức b 3 8 a + 1 = 0 .

Đáp án là B
Cách 1. Sử dụng công thức tính nhanh ta có
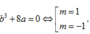
Cách 2. Nhận xét m thỏa mãn thì –m cũng thỏa mãn và hàm số có 3 điểm cực trị khi và chỉ khi m≠ 0 suy ra chọn B

Chọn A
Ta có:
![]()
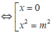
Hàm số (C) có ba điểm cực trị ⇔ m ≠ 0 (*) .
Với điều kiện (*) gọi ba điểm cực trị là:
![]() .
.
Do đó nếu ba điểm cực trị tạo thành một tam giác vuông cân, thì sẽ vuông cân tại đỉnh A.
Do tính chất của hàm số trùng phương, tam giác ABC đã là tam giác cân rồi, cho nên để thỏa mãn điều kiện tam giác là vuông, thì AB vuông góc với AC
![]()
Tam giác ABC vuông khi:
![]()
![]()
![]()
Vậy với m = ± 1 thì thỏa mãn yêu cầu bài toán.
[Phương pháp trắc nghiệm]
Yêu cầu bài toán
⇔ b 3 8 a + 1 = 0 ⇔ - m 6 + 1 = 0
⇔ m = ± 1

Chọn C.
Cách 1: TXĐ: D = ℝ
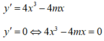
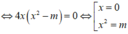
Hàm số đã cho có ba điểm cực trị khi và chỉ khi m > 0 (*)
Với điều kiện (*) đồ thị hàm số có ba điểm cực trị là:
![]()
![]()
Ta có: ![]()
![]()
Suy ra tam giác ABC cân tại A. Do đó tam giác ABC vuông cân tại A
![]()
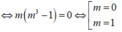
Kết hợp (*) suy ra m = 1.
Cách 2: Áp dụng công thức tính nhanh: Đồ thị hàm số ![]() có ba điểm cực trị là ba đỉnh của một tam giác vuông cân khi và chỉ khi
có ba điểm cực trị là ba đỉnh của một tam giác vuông cân khi và chỉ khi ![]()
Ta có: ycbt
⇔
(
-
2
m
)
3
+
8
=
0
![]()



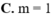
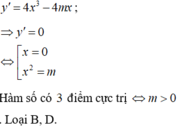
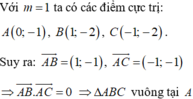
\(y'=4mx^3-8x=0\Rightarrow\left[{}\begin{matrix}x=0\\mx^2=2\end{matrix}\right.\)
Hàm có 3 cực trị khi \(m>0\)
Gọi 3 cực trị là A, B, C với \(\left\{{}\begin{matrix}A\left(0;1\right)\\B\left(\sqrt{\dfrac{2}{m}};1-\dfrac{4}{m}\right)\\C\left(-\sqrt{\dfrac{2}{m}};1-\dfrac{4}{m}\right)\end{matrix}\right.\)
Gọi H là trung điểm BC \(\Rightarrow H\left(0;1-\dfrac{4}{m}\right)\)
\(AH=\left|y_A-y_H\right|=\dfrac{4}{m}\) ; \(BC=\left|x_B-x_C\right|=2\sqrt{\dfrac{2}{m}}\)
Tam giác ABC luôn cân tại A nên nó vuông cân khi \(AH=\dfrac{1}{2}BC\)
\(\Leftrightarrow\dfrac{4}{m}=\sqrt{\dfrac{2}{m}}\Rightarrow m=8\)