Cho tam giác ABC có AB + AC = 2BC. Gọi G, O lần lượt là trọng tâm, điểm cách đều của tam giác ABC. CMR: GO // BC.
HD: Gọi giao điểm của AO và BC là D, giao điểm của AG và BC là N.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

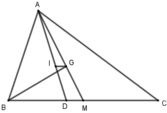
Gọi D, M là giao điểm của AI, AG với BC.
Vì AD là tia phân giác góc B A C ^ nên B D A B = D C A C (t/c)
⇒ B D 12 = D C 18 = B D + D C 12 + 18 = 15 30 = 1 2
=> BD = 12. 1 2 = 6, DC =18. 1 2 = 9
Lại có: BI là tia phân giác A B D ^ nên A I I D = A B B D = 12 6 = 2 (tính chất)
=> I D A D = M G M A = 1 3 hay D đúng
Mà AG = 2GM (vì G là trọng tâm)
Nên A I I D = A G G M = 2 hay B đúng
Theo định lí đảo của định lí Talet ta có:
IG // DM => IG // BC hay A đúng
Chỉ có C sai
Đáp án: C

Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,
ghghhggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggghhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh

a: OM//AH
ON//BH
MN//AB
=>góc BAH=góc OMN và góc ABH=góc ONM
=>ΔABH đồng dạng với ΔMNO
b: A,G,M thẳng hàng và H,G,O thẳng hàng
=>góc AGH=góc MGO
=>ΔAHG đồng dạng với ΔMOG
=>OM/AH=MG/AG
=>OM/AH=MN/AB=1/2
=>GM/GA=1/2
=>G là trọng tâm của ΔACB
Bài hay quá!
Điểm cách đều tam giác ở đây chắc là tâm đường tròn nội tiếp?
Gọi điểm tiếp xúc của đường tròn nội tiếp (O) với hai cạnh BC,AB là D,F. Gọi M là trung điểm của BC và phân giác AO cắt đường tròn ngoại tiếp tam giác ABC ở K.
Ta kí hiệu \(a,b,c\) là độ dài ba cạnh BC,CA,AB như thông thường. Ta có ngay \(b+c=2a,\)(do giả thiết). Mặt khác \(AF=\frac{b+c-a}{2}=\frac{a}{2}=BM\). Mặt khác \(\angle MBK=\frac{\angle A}{2}=\angle FAO\). Suy ra \(\Delta FAO=\Delta MBK\) (cạnh huyền, cạnh góc vuông). Do vậy \(\text{AO=BK, FO=KM}\), suy ra \(OD=KM\). . Gọi \(T=AK\cap BC\) suy ra \(T\) là trung điểm \(KO\).
Cuối cùng để ý rằng \(\angle OBK=\frac{B}{2}+\frac{A}{2}=\angle BOK\to\Delta OBK\) cân ở \(K\), do đó \(KB=KO=KA\to AO=2OT.\) Vậy ta có \(\frac{AO}{OT}=2=\frac{AG}{GN}\to\) theo định lý Ta-let đảo thì OG song song BC.
Bài này hay đến nỗi nên thơ, hay đến nỗi nỗi làm rung động các nhà bác học toán lừng danh trên thế giới