Question

[Nguyễn Thị Tú Linh]

Hai người đi bộ cùng chiều trên một đường thẳng . Người thứ nhất đi với vận tốc không đổi bằng 0,9 m / s . Người thứ 2 đi với vận tốc không đổi bằng 1,9 m / s . Biết 2 người cùng xuất phát tại cùng một vị trí .

a) Nếu người thứ 2 đi không nghỉ thì sau bao lâu sẽ đến một địa điểm cách nơi xuất phát 780m ?

b) Người thứ 2 đi được một đoạn thì dừng lại , sau 5,50 phút thì người thứ nhất đến . Hỏi vị trí cách nơi xuất phát bao xa ?

Answer 1

[Đinh Tuấn Việt]

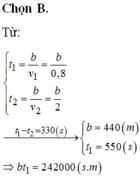
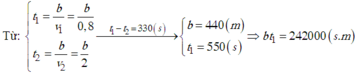
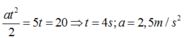
a) Thời gian người thứ hai đến điểm 780m là :
t₂ = \(\frac{780}{1,9}\)  \(\approx\) 410,5 s 

b) 5,50 phút = 300giây + 30giây = 330giây
Gọi t là thời gian người thứ 2 đi => (t+330) là thời gian người thứ nhất đi
Quãng đường người thứ nhất đi: S = 0,9(t+330)
Quãng đường người thứ hai đi: S = 1,9t
=> S = 0,9(t+330) = 1,9t
Ta có phuơng trình: 0,9(t+330)=1,9t; giải hệ có t = 297giây
Vậy vị trí đó cách nơi xuất phát : S =1,9t = 1,9.297 = 564,3m

Answer 2

[ncjocsnoev]

a) Chọn trục tọa độ trùng với dường thẳng chuyển động , gốc tọa độ là vị trí xuất phát , chiều dương là chiều chuyển động , gốc thời gian là thời điểm xuất phát .

   v = \(\frac{\triangle x}{\triangle t}\) → \(\triangle t=\frac{\triangle x}{v}=\frac{780}{1,9}=410,53\left(s\right)=6,84min\) = 6 min 50( s )

b) Gọi t là thời gian người thứ 2 đi cho đến khi dừng lại . Quãng đường người thứ 2 đi được là : S = vt = 1,9t

Cùng trong thời gian t ( s ) , người thứ nhất đi được là : S₁ = v₁t = 0,9t

Quãng đường người thứ nhất đi được kể từ khi người thứ 2 dừng cho tới lúc gặp nhau là : S₂ = v1t` = 0,9 . ( 5,5 . 60 ) 297 ( m )

Ta có : S₁ + S₂ = S  ↔  297 + 0,9t = 1,9t     → t = 297 ( s )

Suy ra : S = 1,9t = 1,9 . 297 = 564,3 ( m )

Vậy vị trí người thứ hai nghỉ cách nơi xuất phát là 564,3 ( m ).