K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

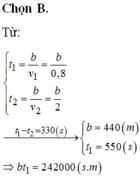
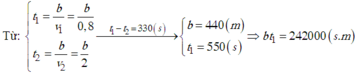


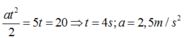
a) Thời gian người thứ hai đến điểm 780m là :
t2 = \(\frac{780}{1,9}\) \(\approx\) 410,5 s
b) 5,50 phút = 300giây + 30giây = 330giây
Gọi t là thời gian người thứ 2 đi => (t+330) là thời gian người thứ nhất đi
Quãng đường người thứ nhất đi: S = 0,9(t+330)
Quãng đường người thứ hai đi: S = 1,9t
=> S = 0,9(t+330) = 1,9t
Ta có phuơng trình: 0,9(t+330)=1,9t; giải hệ có t = 297giây
Vậy vị trí đó cách nơi xuất phát : S =1,9t = 1,9.297 = 564,3m
a) Chọn trục tọa độ trùng với dường thẳng chuyển động , gốc tọa độ là vị trí xuất phát , chiều dương là chiều chuyển động , gốc thời gian là thời điểm xuất phát .
v = \(\frac{\triangle x}{\triangle t}\) → \(\triangle t=\frac{\triangle x}{v}=\frac{780}{1,9}=410,53\left(s\right)=6,84min\) = 6 min 50( s )
b) Gọi t là thời gian người thứ 2 đi cho đến khi dừng lại . Quãng đường người thứ 2 đi được là : S = vt = 1,9t
Cùng trong thời gian t ( s ) , người thứ nhất đi được là : S1 = v1t = 0,9t
Quãng đường người thứ nhất đi được kể từ khi người thứ 2 dừng cho tới lúc gặp nhau là : S2 = v1t` = 0,9 . ( 5,5 . 60 ) 297 ( m )
Ta có : S1 + S2 = S ↔ 297 + 0,9t = 1,9t → t = 297 ( s )
Suy ra : S = 1,9t = 1,9 . 297 = 564,3 ( m )
Vậy vị trí người thứ hai nghỉ cách nơi xuất phát là 564,3 ( m ).