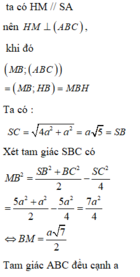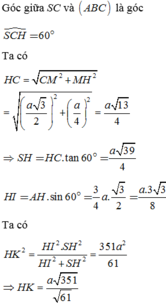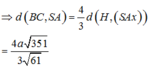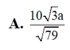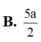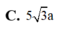Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và SC = 2a√5 . Hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm M của cạnh AB. Góc giữa đường thẳng SC và (ABC) bằng 600. Tính thể tích khối chóp S.ABC theo a.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
QD
Quốc Đạt
31 tháng 5 2016
Đúng(0)
Những câu hỏi liên quan
CM
24 tháng 1 2017
Đáp án A.
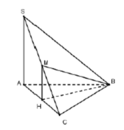
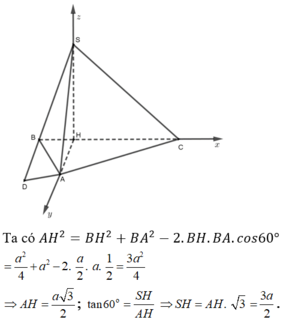
Ta có S C H ^ = 60 ° và
H C = a 7 3 ; S H = H C tan S C H ^ = a 21 3
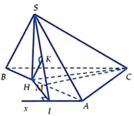
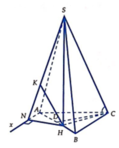
Từ A kẻ tia A x / / C B (như hình vẽ). Khi đó B C / / S A x và do B A = 3 2 H A nên
d B C , S A = d B C , S A x = d B , S A x = 3 2 d H , S A x
Gọi N và K lần lượt là hình chiếu vuông góc của H trên Ax và SN.
Do A N ⊥ S H N và H K ⊥ S N nên H K ⊥ S A N . Khi đó d B C , S A = 3 2 H K .
Ta có
A H = 2 a 3 ; H N = A H sin N A H ^ = a 3 3 .
Suy ra H K = H N . H S H N 2 + H S 2 = a 42 12 . Vậy d B C , S A = a 42 8 .
CM
22 tháng 7 2017
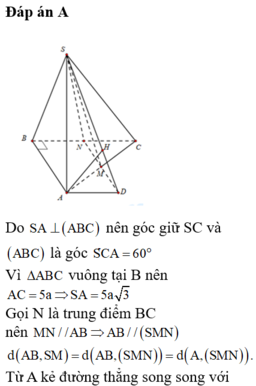
Trong mặt phẳng (ABC), qua A kẻ đường thẳng d song song với BC. Kẻ H I ⊥ d , dễ thấy A I ⊥ S H I . Trong tam giác vuông SHI kẻ H K ⊥ S I , nhận thấy H K ⊥ S I A .
Ta có d S A , B C = d B , S I A = 3 2 d H , S I A = 3 2 H K
Ta tính được H = H A . sin 60 o = a 3 3
Ta có S C H ^ = S C ; A B C ^ , suy ra S H = a 21 3
Từ 1 H K 2 = 1 S H 2 + 1 H I 2 ta thu được H K = a 42 12
Suy ra d S A , B C = 3 2 H K = a 42 8
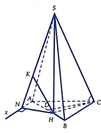
Đáp án C
CM
6 tháng 7 2017
Đáp án D.
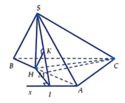
Kẻ Ax//BC, HI ⊥ Ax; HK ⊥ SI.
Gọi M là trung điểm của AB
Ta có AI ⊥ (SHI)=> AI ⊥ HK=> HK ⊥ (SAI)=>d(H,(Sax)) = HK
Góc giữa SC và (ABC) là góc S C H ^ = 60 0
Ta có:
CM
16 tháng 9 2018
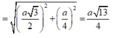
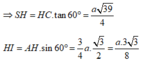
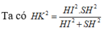
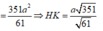
Đáp án D
Phương pháp: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Cách giải: Gọi H là trung điểm của AC
