Tứ giác ABCD có C = 500, D = 600, A : B = 3 : 2. Tính các góc A và B.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 9 2021
1.
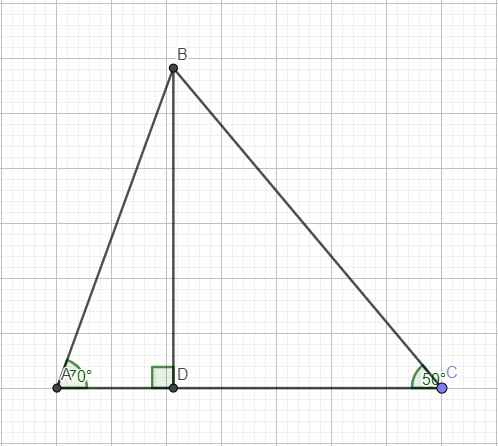
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)
24 tháng 8 2021
a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
\(\Leftrightarrow\widehat{C}+\widehat{D}=210^0\)
mà \(\widehat{C}-\widehat{D}=20^0\)
nên \(2\cdot\widehat{C}=230^0\)
\(\Leftrightarrow\widehat{C}=115^0\)
\(\Leftrightarrow\widehat{D}=95^0\)
Số đo góc ngoài tại đỉnh C là: \(180^0-115^0=65^0\)
b: Ta có: \(\widehat{C}+\widehat{D}=210^0\)
\(\Leftrightarrow\widehat{D}\cdot\dfrac{7}{4}=210^0\)
\(\Leftrightarrow\widehat{D}=120^0\)
\(\Leftrightarrow\widehat{C}=90^0\)
Số đo góc ngoài tại đỉnh C là: \(180^0-90^0=90^0\)
CM
12 tháng 9 2018
a) Sử dụng tính chất dãy tỉ số bằng nhau. A ^ = 144 0 , B ^ = 108 0 , C ^ = 72 0 , D ^ = 36 0
b) Sử dụng tổng ba góc trong tam giác tính được C E D ^ = 126 0 .
Chú ý hai phân giác trong và ngoài tại mỗi góc của một tam giác thì vuông góc nhau, cùng với tổng bốn góc trong tứ giác, ta tính được C F D ^ = 54 0
Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
\(\Leftrightarrow\widehat{A}+\widehat{B}=250^0\)
mà \(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{2}\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{2}=\dfrac{\left(\widehat{A}+\widehat{B}\right)}{5}=\dfrac{250^0}{5}=50^0\)
Suy ra: \(\widehat{A}=150^0\); \(\widehat{B}=100^0\)