Giải giúp mình với ạ, cảm ơn nhiều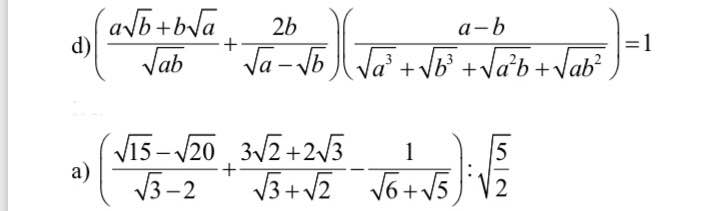
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 10 2021
Bài 6:
a: Xét ΔABC có
D là trung điểm của BC
M là trung điểm của AC
Do đó: DM là đường trung bình của ΔABC
Suy ra: DM//AB và \(DM=\dfrac{AB}{2}=\dfrac{6}{2}=3\left(cm\right)\)
LP
1
HP
30 tháng 10 2021
Đổi 100ml = 0,1 lít
Ta có: \(n_{HCl}=2.0,1=0,2\left(mol\right)\)
a. PTHH: \(AgNO_3+HCl--->AgCl\downarrow+HNO_3\)
Theo PT: \(n_{AgNO_3}=n_{HCl}=0,2\left(mol\right)\)
Đổi 200ml = 0,2 lít
=> \(C_{M_{AgNO_3}}=\dfrac{0,2}{0,2}=1M\)
b. Ta có: \(m_{dd_{HNO_3}}=0,1\left(lít\right)\)
Theo PT: \(n_{HNO_3}=n_{HCl}=0,2\left(mol\right)\)
=> \(C_{M_{HNO_3}}=\dfrac{0,2}{0,1}=2M\)
N
0
83
1
11 tháng 11 2021
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC
hay DECB là hình thang
N
0
AT
16 tháng 7 2021
Ta có: \(AB^2+HC^2=\left(AA'^2+A'B^2\right)+\left(A'H^2+A'C^2\right)\)
\(=\left(AA'^2+A'C^2\right)+\left(A'B^2+A'H^2\right)=AC^2+HB^2\)
Lại có: \(BC^2+HA^2=\left(BB'^2+B'C^2\right)+\left(B'H^2+B'A^2\right)\)
\(=\left(BB'^2+B'A^2\right)+\left(B'C^2+B'H^2\right)=AB^2+HC^2\)
\(\Rightarrow AB^2+HC^2=AC^2+HB^2=BC^2+HA^2\)
PK
5
TA
18 tháng 5 2021
`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)
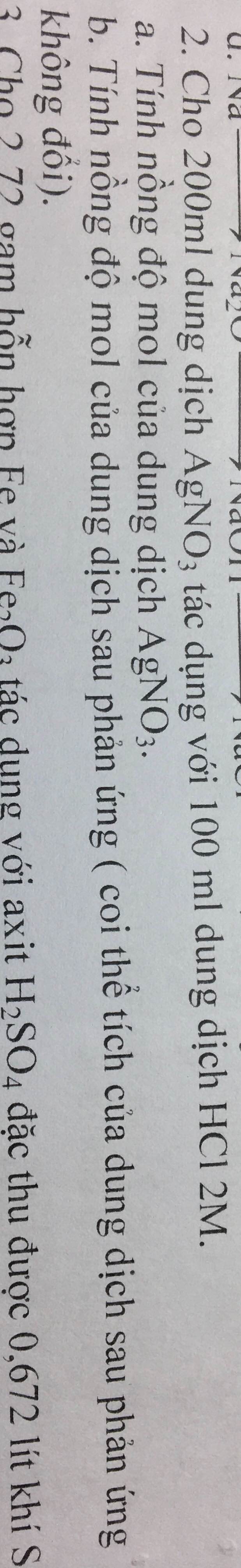
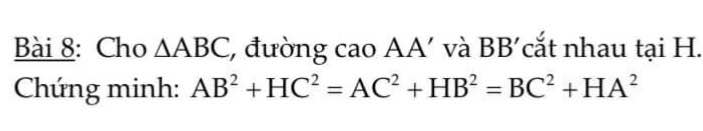
d) Ta có: \(\left(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}+\dfrac{2b}{\sqrt{a}-\sqrt{b}}\right)\left(\dfrac{a-b}{\sqrt{a^3}+\sqrt{b^3}+\sqrt{a^2b}+\sqrt{ab^2}}\right)\)
\(=\left(\sqrt{a}+\sqrt{b}+\dfrac{2b}{\sqrt{a}-\sqrt{b}}\right)\cdot\left(\dfrac{a-b}{a\sqrt{a}+b\sqrt{b}+a\sqrt{b}+b\sqrt{a}}\right)\)
\(=\dfrac{a-b+2b}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{a-b}{\left(\sqrt{a}+\sqrt{b}\right)\left(a+b\right)}\)
\(=\dfrac{\left(a+b\right)\cdot\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\left(a+b\right)\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
=1
Giải tiếp giúp mình luôn câu a với ạ