con lắc đơn dao động điều hòa,m=0,1 kg,g=10,biên độ là 6 độ,chu kì 2s. sau 4 T thì còn lại 4 độ. Để con lắc duy trì dao động bằng 5 độ trong 1 tuần thì cần một công là bao nhiêu,biết 85 % là hao phí
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


@Tuấn: Bởi vì trong dao động tắt dần, độ giảm biên độ sau mỗi chu kỳ thì đều như nhau, nó không phụ thuộc giá trị biên độ lúc đầu.
Còn độ giảm cơ năng thì lại phụ thuộc vào biên độ lúc ban đầu.
Bạn @Tuấn nên gửi mỗi câu thành một bài để anh em dễ trao đổi.
Câu 1:
Vì trong dao động, độ giảm biên độ sau mỗi chu kì là như nhau, nên mỗi chu kỳ, con lắc này giảm: 2/4 = 0,5 độ
Năng lượng dao động của con lắc đơn DĐ ĐH: \(W=\frac{1}{2}m.g.l.\alpha^2\)
Độ giảm năng lượng sau mỗi chu kỳ là: \(\Delta W=W_1-W_2=\frac{1}{2}m.g.l\left(\alpha_1^2-\alpha_2^2\right)=\frac{1}{2}m.\frac{g^2T}{4\pi^2}\left(\alpha_1^2-\alpha_2^2\right)\)
Để duy trì dao động, thì ta cần phải cung cấp cho con lắc trong mỗi chu kỳ là: \(\Delta W\)
Như vậy, năng lượng để cung cấp cho con lắc là: \(E=\Delta W.\frac{7.24.3600}{2}:0,15=739J\)

Chọn B
+ Chu kỳ con lắc:
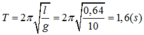
+ Cơ năng ban đầu W0 = mgl(1-cosa0) =

+ Cơ năng sau t = 20T: W = mgl(1-cosa) =

+ Độ giảm cơ năng sau 20 chu kì:

![]()
![]()
+ Công suất trung bình cần cung cấp để con lắc dao động duy trì với biên độ góc là 60
![]()
![]()

Đáp án A
Chu kì dao động của con lắc đơn 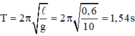
Phần năng lượng bị mất đi sau 10 chu kì
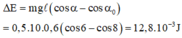
→ Công suất trung bình ![]() = 0,83 mW
= 0,83 mW


Lượng năng lượng trung bình mà dao động mất đi trong mỗi giây
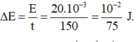
Năng lượng cần để thắng lực cản trong 14 ngày
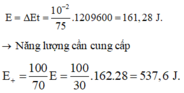
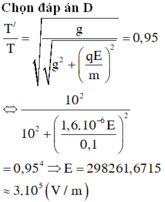
Đáp án D
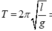
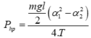
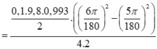


Năng lượng của con lắc đơn: \(W=\frac{1}{2}mgl\alpha_0^2\)(\(\alpha_0\) tính theo rad)
Mà \(l=\frac{g}{\omega^2}\)
\(\Rightarrow W=\frac{1}{2}m\frac{g^2\alpha_0^2}{\omega^2}\)
Độ giảm biên độ của con lắc đơn (hoặc lò xo) sau mỗi chu kì là như nhau, ta gọi là \(\Delta A\)
Như vậy \(4\Delta A=\left(6-4\right)\)\(\Rightarrow\Delta A=0,5^0\)
Để duy trì dao động của con lắc thì ta cần cung cấp cho nó năng lượng đúng bằng năng lượng nó đã mất sau mỗi chu kì, năng lượng này bằng:
\(\Delta E=\frac{1}{2}m\frac{g^2}{\omega^2}\left(\alpha_0^2-\alpha_1^2\right)=\frac{1}{2}m\frac{g^2.T^2}{4\pi^2}\left(\alpha_0^2-\alpha_1^2\right)\)
(\(\alpha_0=5^0;\alpha_1=4,5^0\))
Công suất cần cung cấp: \(P=\frac{\Delta E}{T}=\frac{1}{2}m\frac{g^2.T}{4\pi^2}\left(\alpha_0^2-\alpha_1^2\right)\)
Năng lượng toàn phần cần cung cấp trong một tuần:
\(Q=P.t=\frac{1}{2}0,1\frac{10^2.2}{4.\pi^2}\left(\left(\frac{5\pi}{180}\right)^2-\left(\frac{5,5.\pi}{180}\right)^2\right).7.24.3600:0,85=261J\)
Bạn tính lại xem kết quả đúng không nhé :)