Tìm giá trị của x thỏa mãn:
c, \(\dfrac{x-1}{4}=\dfrac{-9}{1-x}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
L3
3
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 4 2021
\(B=\dfrac{2^2}{x}+\dfrac{3^2}{y}\ge\dfrac{\left(2+3\right)^2}{x+y}=25\)
\(B_{min}=25\) khi \(\left(x;y\right)=\left(\dfrac{2}{5};\dfrac{3}{5}\right)\)
8 tháng 12 2021
a) A = \(\dfrac{1}{x-1}-\dfrac{4}{x+1}+\dfrac{8x}{\left(x-1\right)\left(x+1\right)}\)
= \(\dfrac{x+1-4x+4+8x}{\left(x-1\right)\left(x+1\right)}=\dfrac{5x+5}{\left(x-1\right)\left(x+1\right)}=\dfrac{5}{x-1}\) => đpcm
b) \(\left|x-2\right|=3=>\left[{}\begin{matrix}x-2=3< =>x=5\left(C\right)\\x-2=-3< =>x=-1\left(L\right)\end{matrix}\right.\)
Thay x = 5 vào A, ta có:
A = \(\dfrac{5}{5-1}=\dfrac{5}{4}\)
c) Để A nguyên <=> \(5⋮x-1\)
| x-1 | -5 | -1 | 1 | 5 |
| x | -4(C) | 0(C) | 2(C) | 6(C) |
LD
17 tháng 5 2021
1. \(x=\frac{1}{9}\) thỏa mãn đk: \(x\ge0;x\ne9\)
Thay \(x=\frac{1}{9}\) vào A ta có:
\(A=\frac{\sqrt{\frac{1}{9}}+1}{\sqrt{\frac{1}{9}}-3}=-\frac{1}{2}\)
2. \(B=...\)
\(B=\frac{3\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\frac{4x+6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{3x-9\sqrt{x}+x+3\sqrt{x}-4x-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
3. \(P=A:B=\frac{\sqrt{x}+1}{\sqrt{x}-3}:\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\frac{\sqrt{x}+3}{-6}\)
Vì \(\sqrt{x}+3\ge3\forall x\)\(\Rightarrow\frac{\sqrt{x}+3}{-6}\le\frac{3}{-6}=-\frac{1}{2}\)
hay \(P\le-\frac{1}{2}\)
Dấu "=" xảy ra <=> x=0
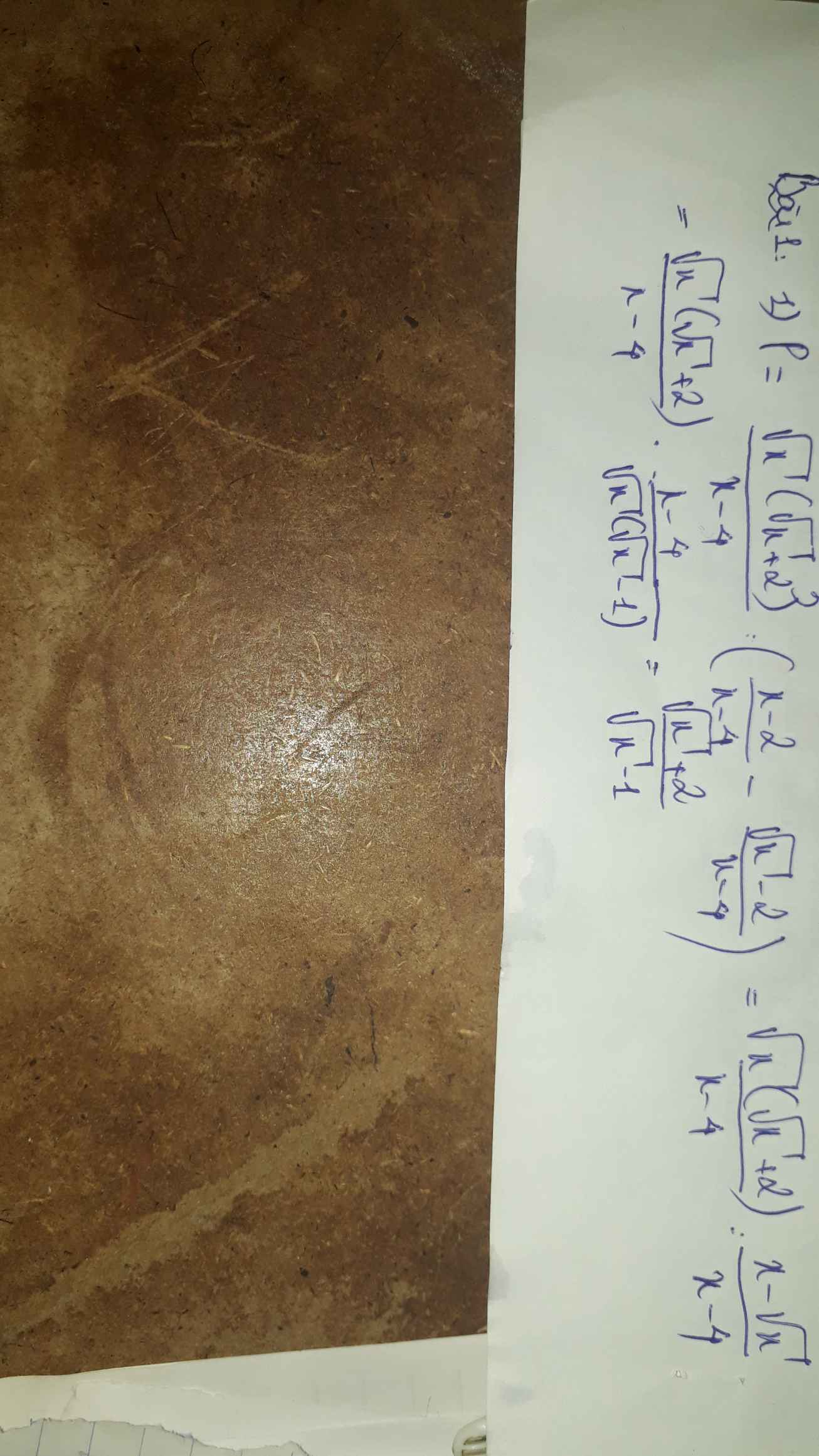
\(\dfrac{x-1}{4}=\dfrac{-9}{1-x}\) (ĐKXĐ:\(x\ne1\))
\(\Leftrightarrow\left(x-1\right)\left(1-x\right)=\left(-9\right).4\)
\(\Leftrightarrow x-x^2-1+x=-36\)
\(\Leftrightarrow-x+x^2+1-x-36=0\)
\(\Leftrightarrow x^2-2x-35=0\)
\(\Leftrightarrow x^2+5x-7x-35=0\)
\(\Leftrightarrow\left(x^2+5x\right)-\left(7x+35\right)=0\)
\(\Leftrightarrow x\left(x+5\right)-7\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\x-7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=7\end{matrix}\right.\)(TMĐK)
Vậy với x=-5 hoặc x=7 thì biểu thức trên thỏa mãn
`(x-1)/4=(-9)/(1-x)`
`(x-1)(1-x)=-9.4`
`(x-1)(x-1)=36`
`(x-1)(x-1)=6.6=(-6).(-6)`
`[(x-1=6),(x-1=-6):}`
`[(x=7),(x=-5):}`