Cmr :2n3 + 3n2 + n chia hết cho 6 với mọi số nguyên n
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = n 4 – 2 n 3 – n 2 +2n = (n – 2)(n – 1)n(n + 1) là tích của 4 số nguyên liên tiếp do đó A ⋮ 24 .

\(n^3+3n^2+2n=n\left(n^2+3n+2\right)=n\left(n+1\right)\left(n+2\right)⋮6\) (vì là 3 số nguyên lt)
\(n^3+3n^2+2n-n\left(n^2+3n+2\right)\)
\(=n\left[n\left(n+1\right)+2\left(n+1\right)\right]=n\left(n+1\right)\left(n+2\right)\)
Là tích 3 số nguyên liên tiếp nên có một số chia hết cho 2 và một số chia hết cho 3
\(\Rightarrow n^3+3n^2+2n=n\left(n+1\right)\left(n+2\right)⋮2.3=6\forall n\in Z\)

Ta có: u n = − 2 n 3 + 3 n 2 + 4 n 4 + 4 n 3 + n = − 2 n 3 + 3 n 2 + 4 n 4 n 4 + 4 n 3 + n n 4 = − 2 n + 3 n 2 + 4 n 4 1 + 4 n + 1 n 3
Mà lim 2 n = 0 , lim 3 n 2 = 0 , lim 4 n 4 = 0 , lim 4 n = 0 v à lim 1 n 3 = 0
Do đó lim u n = 0 + 0 + 0 1 + 0 + 0 = 0
Chọn đáp án B

n3-n=n(n2-1)=n(n+1)(n-1)
Do n là số nguyên =>n-1 ; n ; n+1 là 3 số nguyên liên tiếp nên trong đó tồn tại 1 số chia hết cho 2 và 1 số chia hết cho 3
Mà ƯCLN(2;3)=1
=>n(n-1)(n+1) chia hết cho 2.3 hay chia hết cho 6 với mọi n nguyên
Ta có: n3-n=n.(n2-1)=n.(n-1).(n+1)=(n-1).n.(n+1)
Vì (n-1) và n là 2 số tự nhiên liên tiếp=>(n-1).n chia hết cho 2=>(n-1).n.(n+1) chia hết cho 2(1)
Vì (n-1),n và n+1là 3 số tự nhiên liên tiếp=>(n-1).n.(n+1) chia hết cho 3(2)
Từ (1) và (2) ta thấy:
(n-1).n.(n+1) chia hết cho 2,3.
mà (2,3)=1
=>(n-1).n.(n+1) chia hết cho 6
=>n3-n chia hết cho 6
=>ĐPCM

\(\left(n-1\right)^2\cdot\left(n+1\right)+\left(n^2-1\right)\)
\(=\left(n-1\right)\left(n+1\right)\left(n-1+1\right)\)
\(=n\left(n-1\right)\left(n+1\right)\)
Vì n;n-1;n+1 là ba số nguyên liên tiếp
nên \(n\left(n-1\right)\left(n+1\right)⋮3!\)
hay \(n\left(n-1\right)\left(n+1\right)⋮6\)
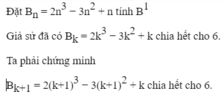
2n3 + 3n2 + n = 2n3 + 2n2 + n2 + n
= 2n ( n+1 ) + n ( n+1) = 3n ( n+1)
Vì n là số nguyên nên n và n+1 là 2 số nguyên liên tiếp
=> 1 trong 2 số n và n+1 có 1 số chẵn
=> n(n+1) chia hết cho 2. Mà 2 và 3 là 2 số nguyên tố cùng nhau
=> 3.n(n+1) chia hết cho 2.3=6 hay 2n3 + 3n2 +n chia hết cho 6 với mọi số nguyên n