Tính A = Sin2 10 độ + Sin2 20 độ +.... + Sin2 70 độ + Sin2 80 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
8 tháng 8 2021
a) sin230 độ - sin240 độ - sin250 độ + sin2 60 độ
= cos260o - cos250o - sin250o + sin260o
= (cos260o + sin260o) - (cos250o + sin250o)
= 1 - 1 = 0
b) cos225 độ - cos235độ + cos245 độ -cos2 55 độ + cos2 65 độ
= sin265o - sin255o + cos245o - cos255o + cos265o
= (sin265o + cos265o) - (sin255o + cos255o) + cos245o
= 1 - 1 +1/2
= 1/2
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
Sử dụng 2 công thức: \(sina=cos\left(90^0-a\right)\) và \(sin^2a+cos^2a=1\) ta có:
\(A=sin^25^0+cos^2\left(90^0-85^0\right)=sin^25^0+cos^25^0=1\)
CM
8 tháng 10 2019
Đáp án B
Theo giả thiết có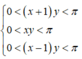 
và
Và thay vào đẳng thức điều kiện có:
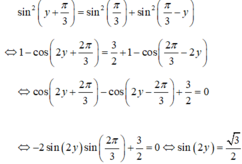
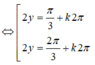
Đối chiếu với điều kiện nhận 
NH
0
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 2 2021
\(S_{HKE}=S_{ABC}-S_{AKE}-S_{BHE}-S_{CHK}\)
\(\Leftrightarrow\dfrac{S_{HKE}}{S_{ABC}}=1-\dfrac{S_{AKE}}{S_{ABC}}-\dfrac{S_{BHE}}{S_{ABC}}-\dfrac{S_{CHK}}{S_{ABC}}\)
\(\Leftrightarrow\dfrac{1}{4}=1-\dfrac{\dfrac{1}{2}AE.AK.sinA}{\dfrac{1}{2}AB.AC.sinA}-\dfrac{\dfrac{1}{2}BH.BE.sinB}{\dfrac{1}{2}AB.BC.sinB}-\dfrac{\dfrac{1}{2}CH.CK.sinC}{\dfrac{1}{2}AC.BC.sinC}\)
\(\Leftrightarrow\dfrac{AE.AK}{AB.AC}+\dfrac{BH.BE}{AB.BC}+\dfrac{CH.CK}{AC.BC}=\dfrac{3}{4}\)
(Để ý rằng \(\dfrac{AE}{AC}=cosA\) do tam giác ACE vuông tại E và tương tự...)
\(\Leftrightarrow cosA.cosA+cosB.cosB+cosC.cosC=\dfrac{3}{4}\)
\(\Leftrightarrow cos^2A+cos^2B+cos^2C=\dfrac{3}{4}\)
\(\Leftrightarrow1-sin^2A+1-sin^2B+1-sin^2C=\dfrac{3}{4}\)
\(\Leftrightarrow sin^2A+sin^2B+sin^2C=\dfrac{9}{4}\)
2 tháng 11 2021
\(a,A=\left(\cos^220^0+\cos^270^0\right)+\left(\cos^240^0+\cos^250^0\right)\\ A=\left(\cos^220^0+\sin^220^0\right)+\left(\cos^240^0+\sin^240^0\right)=1+1=2\\ b,B=\left(\cos^2\alpha\right)^3+\left(\sin^2\alpha\right)^3+3\sin^2\alpha\cdot\cos^2\alpha\cdot\left(\sin^2\alpha+\cos^2\alpha\right)\\ B=\left(\sin^2\alpha+\cos^2\alpha\right)^3=1^3=1\)
A = ( sin2 10o + sin2 80o) + (sin2 20o + sin2 70o) + ...+ (sin240o + sin2 50o)
A = ( sin2 10o + cos2 10o) + (sin2 20o + cos2 20o) + ...+ (sin240o + cos2 40o)
A = 1 + 1 + 1 + 1 = 4 ( Vì ( sin2 a + cos2 a = 1 với mọi a)
Bài làm
A = ( sin2 10o + sin2 80o) + (sin2 20o + sin2 70o) + ...+ (sin240o + sin2 50o)
A = ( sin2 10o + cos2 10o) + (sin2 20o + cos2 20o) + ...+ (sin240o + cos2 40o)
A = 1 + 1 + 1 + 1 = 4
hok tốt